Introducere
Întâlnim pentru prima dată cuvântul „trigonometrie” în cartea „Trigonometria: sive de solutione triangulorum tractatus brevis et perspicuus” publicată de Bartholomaeus Pitiscus în 1595. Trigonometrie înseamnă „măsurarea trigoanelor” și provine din cuvintele grecești trigonon („triunghi”) și metron („a măsura”). Astfel, funcțiile trigonometrice sunt funcții care reprezintă relația dintre laturile și unghiurile unui triunghi.
Funcțiile trigonometrice ale unui unghi, cel mai utilizate astăzi, sunt sinusul (sin), cosinusul (cos) și tangenta (tg sau tan). Ele sunt urmate de inversele lor cosecantă (cosec sau csc), secantă (sec) și cotangentă (ctg sau cot). Aceste funcții trigonometrice sunt descrise în figura de mai jos folosindu-se un triunghi dreptunghic.
Se consideră triunghiul ABC, dreptunghic în A, cu unghiurile ascuțite B și C. Notăm cu a lungimea ipotenuzei (latura opusă unghiului drept A ). Iar cu b și c lungimile catetelor opuse unghiurilor B și respectiv C.
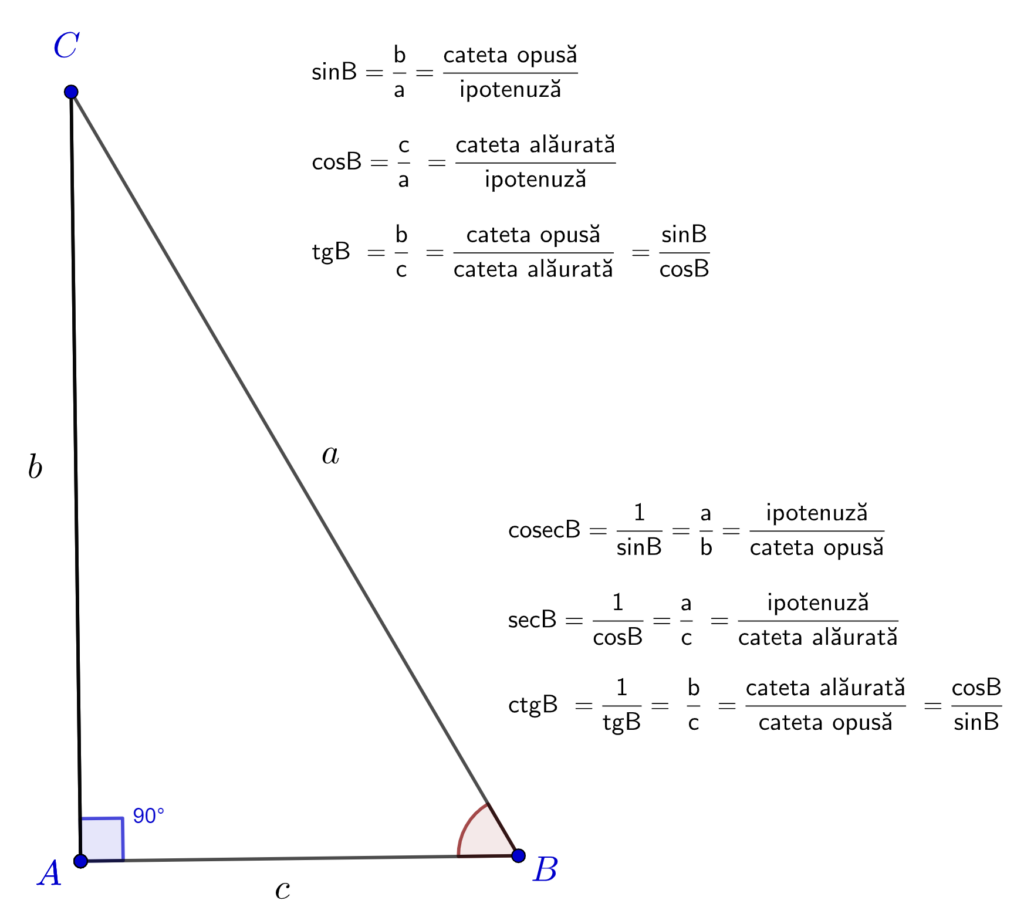
si inversele lor cosecantă (cosec), secantă (sec) și cotangentă (ctg).
Funcțiile trigonometrice definite direct în termeni de triunghiuri dreptunghice, apar prima dată în secolul al XVI-lea în lucrările lui Joachim Rheticus. Iar notațiilor moderne pentru funcțiile trigonometrice așa cum le folosim astăzi apar mai târziu, în secolul al XVIII-lea fiind introduse de Leonhard Euler.
Valorile funcțiilor trigonometrice pentru unghiurile de 0^\circ, 30^\circ, 45^\circ, 60^\circ, 90^\circ și 180^\circ care sunt foarte cunoscute astăzi sunt o mărturie a evoluției gândirii de-a lungul istoriei.
\begin{array}{|c|c|c|c|}
\hline \\
\text{Unghi/Funcție} & \sin & \cos & \tg \\[9pt]
\hline \\
\displaystyle{0} \, \left(0^\circ\right) & 0 & 1 & 0 \\[9pt]
\hline \\
\displaystyle{\frac{\pi}{6}} \, \left(30^\circ\right) & \displaystyle\frac{1}{2} & \displaystyle\frac{\sqrt{3}}{2} & \displaystyle\frac{\sqrt{3}}{{3}} \\[9pt]
\hline \\
\displaystyle\frac{\pi}{4} \, \left(45^\circ\right) & \displaystyle\frac{\sqrt{2}}{2} & \displaystyle\frac{\sqrt{2}}{2} & 1 \\[9pt]
\hline \\
\displaystyle\frac{\pi}{3} \, \left(60^\circ\right) & \displaystyle\frac{\sqrt{3}}{2} & \displaystyle\frac{1}{2} & \sqrt{3} \\[9pt]
\hline \\
\displaystyle\frac{\pi}{2} \, \left(90^\circ\right) & 1 & 0 & \text{Nedefinit} \\[9pt]
\hline \\
\displaystyle\pi \, \left(180^\circ\right) & 0 & -1 & 0 \\[9pt]
\hline
\end{array}Originea și evoluția trigonometriei sunt adesea lăsate în umbră. Funcțiile trigonometrice, precum sinusul, chiar dacă nu erau definite ca în zilele noastre, erau folosite în astronomie de către babilonieni, egipteni și greci în antichitate.
În continuare vom prezenta o scurtă istorie a funcțiilor trigonometrice din antichitate până în era digitală.
Funcțiile trigonometrice în antichitate
Babilonul
În absența unei teorii formale a trigonometriei, civilizația babiloniană a recurs la metode empirice pentru a gestiona măsurătorile unghiurilor și ale laturilor triunghiurilor dreptunghice. Aceste cunoștințe erau meticulos consemnate pe tăblițe de lut, martori ai ingeniozității lor matematice.

Un exemplu remarcabil în acest sens este tăblița Plimpton 322, care se distinge prin înregistrarea a cincisprezece triplete pitagorice. Aceasta conține și o serie de numere organizate într-o manieră ce sugerează un tabel de secante.
Babilonienii au adoptat un sistem de numerație sexagesimal (în baza 60), unul dintre primele care a utilizat un principiu pozițional pentru reprezentarea numerelor. Valoarea fiecărui simbol depindea de poziția sa în număr, similar cu sistemul decimal folosit astăzi. Acest sistem de numărare, datorită capacității sale remarcabile de divizibilitate, a facilitat efectuarea calculelor complexe. Sistemul sexagesimal a fost extensiv utilizat în calculele astronomice. Iar cunoștințele babiloniene care au fost transmise mai departe au influențat dezvoltarea ulterioară a trigonometriei. Multe din convențiile noastre moderne legate de măsurarea timpului (60 de secunde într-un minut, 60 de minute într-o oră) și divizarea cercurilor în 360∘ de grade derivă din sistemul babilonian. Astfel babilonienii au pus fundamentele explorării matematice viitoare, contribuind semnificativ la evoluția trigonometriei.
Grecia Antică
Progresul timpuriu în trigonometrie s-a produs în trigonometria sferică, în mare parte datorită aplicației sale în astronomie.
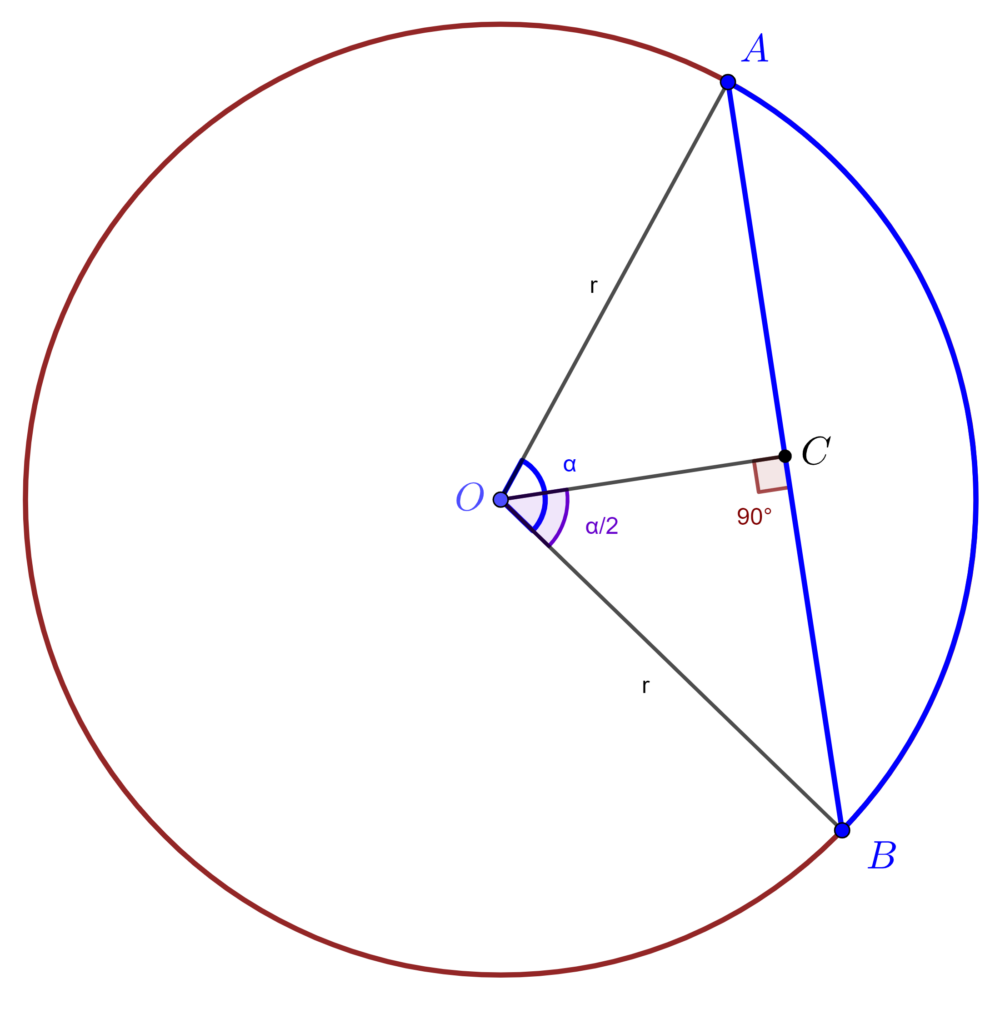
Astronomii și matematicienii greci construiau tabele de lungimi de coarde cu o divizare a cercului în 360∘. Pentru aceasta, alegeau o rază de dimensiune fixă. Aceste tabele asociază fiecărei valori a unghiului la centru lungimea corzii. Aceste valori corespund dublului sinusului unghiului la jumătate. Fiind precursoare ale funcției sinus, erau utilizate în formule echivalente cu formulele actuale pentru funcțiile trigonometrice. Tabele de coarde au fost rafinate și organizate în mod progresiv. Acest lucru a culminat cu stabilirea definițiilor și notațiilor moderne pentru funcțiile trigonometrice în secolul al XVII-lea.
Hipparchus
Astronomii antici greci, printre care se numără și Hipparchus din Niceea, (190-120 î.Hr) sunt recunoscuți pentru contribuțiile semnificative în dezvoltarea trigonometriei. Hipparchus, adesea considerat fondatorul trigonometriei, a creat primele tabele de valori corespunzătoare coardelor pentru o serie de unghiuri. Pentru calculele sale el folosește împărțirea cercului în 360∘, iar cantitățile mai mici decât gradele sub forma fracțiilor sexagesimale după modelul babilonian. Astfel fiecare grad este împărțit în 60 de minute și fiecare minut este împărțit în 60 de secunde.
Hipparchus folosește aceste tabele pentru calculele astronomice. Tabelele de coarde folosite împreuna cu rapoartele deja cunoscute ale triunghiurile asemenea devin instrumente de calcul indispensabile pentru calculele atât astronomice cât și matematice. Se crede că Hipparchus este primul care a determinat exact momentele răsăritului și apusului semnelor zodiacale folosindu-se de aceste tabele de coarde.
În timpul lui Hipparchus, formulele de bază ale trigonometriei plane erau exprimate în termeni pur geometrici ca relații între diferitele coarde și unghiurile (sau arcele) care le subîntind. În următoarele câteva secole trigonometria s-a bazat pe calculul acestor tabele de coarde.
Ptolemeu
Aceste tabele de coarde ne-au fost transmise prin munca lui Ptolemeu(100-168 e.n.), care a preluat și aprofundat cercetările lui Hipparchus. Ptolemeu a completat și rafinat tabelele de coarde existente. În tabelele sale se regăsesc valori pentru unghiuri cuprinse între o jumătate de grad, \frac{1}{2}^\circ , și 180° din jumătate in jumătate de grad (0- zero nu este încă inventat) și au fost cuprinse în cartea sa Almagest, un compendiu despre astronomie.
Pentru calculele sale, Ptolemeu, a folosit un cerc de rază r = 60 de unități deoarece a folosit sistemul de numerație sexagesimal babilonian (baza 60) atât pentru unghiuri, cât și pentru lungimi. Un cerc cu raza de 60 de unități se potrivește bine acestui sistem. Astfel obține AB= 120 ⋅sin \frac{\alpha}{2}. Deci prin dublarea arcului vom putea obține un tabel al valorilor funcției sin, excluzând factorul de proporționalitate de 120. Ptolemeu a îmbunătățite astfel tabelele deja existenta ale lui Hipparchus folosindu-se și de formule precum cea care va fi mai târziu cunoscută sub numele de Teorema lui Ptolemeu. Această teoremă spune că, dacă ABCD este un patrulater inscriptibil, produsul lungimilor diagonalelor este egal cu suma produselor lungimilor celor două perechi de laturi opuse.
Aplicând trigonometria în analiza sferei celeste, Ptolemeu a dezvoltat trigonometria sferică. Aceasta este esențială pentru determinarea unghiurilor și distanțelor pe suprafețe sferice, precum Pământul sau bolta cerească. Dezvoltarea trigonometriei sferice are implicații majore în domeniile navigației și cartografiei. „Almagest”, opera emblematică a lui Ptolemeu, devine baza concepției umanității despre lume până la mijlocul secolului al XVI-lea. Abia atunci, sistemul heliocentric al lui Nicolaus Copernicus va înlocui sistemul geocentric al lui Ptolemeu.
Funcțiile trigonometrice în evul mediu
Contribuțiile indiene
Aryabhata I, un eminent matematician și astronom din India secolului al V-lea e.n., a contribuit semnificativ la progresul trigonometriei. Recunoscut ca unul dintre pionierii utilizării funcțiilor trigonometrice, Aryabhata a prezentat în lucrarea sa „Aryabhatiya” conceptele de sin (jya), cos (kojya), versin (1-cos) (utkrama-jya) și o formă timpurie a tangentei. Aceste noțiuni au stat la baza dezvoltării funcțiilor trigonometrice așa cum le cunoaștem azi.

Mai mult, Aryabhata a creat tabele de valori pentru funcția sinus mult mai precise. Astfel îmbunătățește realizarea calculelor în domeniul astronomiei și trigonometriei.
Alți matematicieni indieni au continuat lucrările lui Aryabhata în studiul trigonometriei. Varahamihira descoperă formulele bine cunoscute acum:
sin^2 x +cos^2 x = 1 \ \\ \ \\ sin \ x = cos (90^\circ -x) \ \\ \ \\ \frac{1}{2}(1 - cos2x) = sin^2xInfluența lumii islamice
Lucrările indiene au fost traduse si îmbunătățite de matematicienii lumii islamice.
Al-Battani (858 – 929 e.n.) cunoscut ca Albategnius, se distinge ca fiind unul dintre astronomii și matematicienii de frunte din perioada medievală islamică. Opera sa a exercitat o influență notabilă asupra evoluției științelor exacte, atât în contextul islamic, cât și în cel european medieval.
Anterior introdusă în matematica indiană, funcția sinus a fost rafinată de Al-Battani. El a amplificat înțelegerea și tehnicile de calcul asociate, contribuind astfel la progresul trigonometriei ca domeniu fundamental al matematicii. Prin elaborarea unor tabele de sinusuri extrem de precise, bazate pe diviziunea cercului în 360 de grade, Al-Battani a ușurat semnificativ efectuarea calculelor astronomice și trigonometrice.
Este de-asemenea cunoscută regula sa pentru determinarea unghiului α de elevație a Soarelui deasupra orizontului în funcție de lungimea l a umbrei proiectate de un gnomon (cel mai vechi tip de cadran solar) vertical de înălțime ℎ astfel:
l = h\frac{ \sin(90^\circ - \alpha)}{\sin \alpha}\ \\ \
Formulă este echivalentă cu l =h\cdot ctg(\alpha). Plecând de la această regulă a creat un tabel al umbrelor. Practic, acesta este un tabel al valorilor cotangentelor, pentru unghiuri de la 1° la 90 °.

În plus, Al-Battani a inovat prin dezvoltarea metodelor de calcul necesare rezolvării ecuațiilor trigonometrice. Acestea l-au ajutat în contextul astronomic la determinarea pozițiilor corpurilor cerești și calculul eclipselor.
Abu Al-Wafa (940-998 e.n) este un matematician persan în ale cărui lucrări se regăsesc fiecare dintre cele șase funcții trigonometrice precum și tabele de valori pentru funcția sinus. Aceste valori fiind calculate la intervale de 0,25°, cu 8 zecimale exacte. De asemenea, se regăsesc și tabele ale valorilor funcției tangente precum și formula :
sin(2\alpha)=2\cdot sin\alpha\cdot cos\alpha
Abu Al-Wafa a prezentat formula trigonometrice pentru calcularea valorii sinusului sumei sau diferenței a doua unghiuri cu demonstrație completă:
sin(\alpha \pm \beta) = \sqrt[]{sin^2 \alpha -(sin\alpha \ sin\beta)^2}\pm\sqrt[]{sin^2 \beta -(sin\alpha \ sin\beta)^2}Formula este cunoscută astăzi sub forma:
sin(\alpha \pm \beta) = sin\alpha \cos\beta\pm cos\alpha sin\beta
Teorema sinusurilor
Nasir al‐Din al‐Tusi (1201-1274e.n), a formulat si demonstrat teorema sinusurilor pentru triunghiuri plane. În trigonometrie, teorema sinusurilor este o relație de proporționalitate între lungimile laturilor unui triunghi și sinusurile unghiurilor respective opuse.
Fie triunghiului oarecare ABC. Notăm cu a lungimea laturii opuse unghiului A. Notăm cu b lungimea laturii opuse unghiurilor B. Notăm cu c lungimea laturii opuse unghiului C. Notăm cu R raza cercului circumscris triunghiului ABC ca in figura de mai jos:
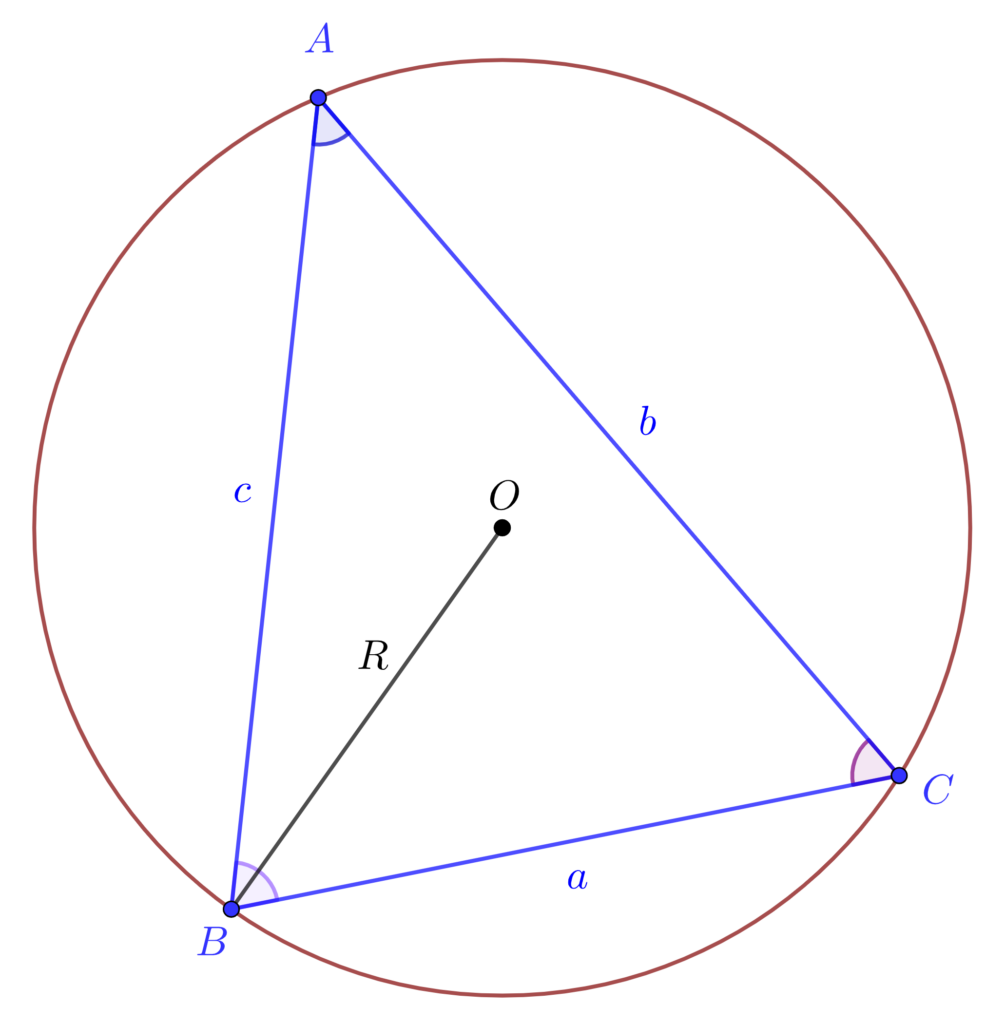
atunci vom avea relațiile:
\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}=2 R
Funcțiile trigonometrice în Europa medievală și renaștere
Regiomontanus -prima opera dedicată exclusiv trigonometriei
Johannes Müller von Königsberg (1436 – 1476) cunoscut sub numele de Regiomontanus, a fost un pionier în abordarea trigonometriei ca o disciplină matematică distinctă, independentă de astronomie. Aceasta reprezintă una dintre contribuțiile sale cele mai semnificative la dezvoltarea științelor. Lucrarea sa fundamentală, „De triangulis omnimodis” (Despre triunghiuri de toate felurile), redactată în 1464, a fost publicată postum în 1533. Lucrarea a jucat un rol esențial în evoluția trigonometriei, sistematizând și extinzând baza de cunoștințe existentă în domeniu.
Această operă este prima dedicată integral trigonometriei. „Despre triunghiuri de toate felurile” oferă o abordare sistematică pentru rezolvarea triunghiurilor, fie că sunt în plan sau pe sferă, tratându-le ca pe o problemă strict matematică. În această lucrare, aspectele de astronomie nu sunt abordate. Regiomontanus se concentrează pe prezentarea cunoștințele geometrice necesare utilizării ulterioare în astronomie. A introdus teoreme importante legate de triunghiul dreptunghic și nu numai, și metodologii matematice avansate pentru determinarea unghiurilor și distanțelor. Acesta este motivul pentru care structura lucrării „Despre triunghiuri de toate felurile” reflectă tradiția geometrică clasică. Lucrarea, similară cu „Elementele” lui Euclid, diferă de operele astronomice, cum ar fi „Almagestul” lui Ptolemeu marchează momentul in care se pun temeliile trigonometriei moderne.
În plus, prin promovarea tipăririi lucrărilor științifice, a facilitat răspândirea cunoștințelor matematice și științifice în Europa, contribuind la accesibilitatea acestora.
Joachim Rheticus
Georg Joachim Rheticus (1514–1576) este cunoscut mai ales pentru rolul său de discipol și promotor al lui Nicolaus Copernicus și al sistemului său heliocentric. Una dintre realizările majore ale lui Rheticus în trigonometrie a fost publicarea lucrării „Canon doctrinæ triangulorum” în 1551.

Canon doctrinae triangulorum
sursa Österreichische Nationalbibliothek
Autor Georg Joachim Rheticus
Tratatul „Canon doctrinæ triangulorum” a fost prima lucrare în care funcțiile trigonometrice erau definite direct în termeni de triunghiuri dreptunghice în loc de cercuri. In acest tratat Rheticus a inclus si tabele ale celor șase funcții trigonometrice. O versiune extinsă a acestui tratat a fost finalizată în 1596 de Valentin Otho, un elev al lui Rheticus.
Trigonometria de la geometrie la geometrie analitică
În secolul al XVI-lea, trigonometria și-a început transformarea dintr-o disciplină pur geometrică într-un subiect algebric-analitic. Această schimbare a fost stimulată de apariția algebrei moderne, inițiată de matematicianul francez François Viète (1540–1603). Folosindu-se de aceasta, alți doi gânditori francezi, Pierre de Fermat(1607-1665) și René Descartes(1596-1650), au pus bazele dezvoltării geometriei analitice.
François Viète
François Viète a fost primul care a formulat explicit relațiile trigonometrice între lungimile laturilor unui triunghi în termeni de rapoarte. A introdus acest concept în lucrarea sa „Canon Mathematicus seu Ad triangula” (Canonul Matematic sau Despre Triunghiuri), publicată în 1579. Această lucrare a adus o contribuție semnificativă în domeniul trigonometriei. Ea conține tabele trigonometrice detaliate și metode de calcul trigonometric, consolidând astfel înțelegerea relațiilor dintre unghiuri și laturi în triunghiuri.
Prin această nouă abordare, Viète a ușurat în mod semnificativ calculul soluțiilor ecuațiilor trigonometrice și algebrice. Astfel matematicienii nu mai erau nevoiți să recurgă la metode geometrice complicate și mai puțin intuitive pentru a aborda problemele trigonometrice. În schimb, puteau aplica direct relații algebrice între elementele triunghiurilor, facilitând rezolvarea ecuațiilor trigonometrice și algebrice, inclusiv a celor polinomiale.

colecție a lucrărilor lui François Viète
publicată postmortem la Leiden în 1646
de Bonaventure și Abraham Elzevier.
François Viète este adesea considerat părintele algebrei moderne. El a introdus sistemul de notație algebric și utilizarea literelor pentru reprezentarea constantelor și variabilelor în ecuații. Această inovație a permis o manipulare mai flexibilă și mai abstractă a conceptelor matematice. Regăsim toate acestea în lucrarea sa „In artem analyticem isagoge” (Introducere în arta analitică), publicată în 1591.
În lucrările sale, Viète a arătat că soluțiile multor ecuații algebrice pot fi exprimate prin intermediul funcțiilor trigonometrice. El a dezvoltat metode pentru rezolvarea ecuațiilor de gradul al doilea, al treilea și al patrulea. Utilizând funcții trigonometrice, Viète dezvoltă metode pentru a găsi rădăcinile reale ale acestor ecuații.
Astfel pune bazele unei noi metode de abordare a problemelor algebrice complexe. Această metodă deschide calea pentru integrarea algebrei cu trigonometria și analiza matematică. Ea devine instrumentul preferat pentru explorarea proprietăților algebrice pregătind terenul pentru ceea ce va fi identitatea lui Euler.
Pierre de Fermat și René Descartes
Invenția geometriei analitice este atribuită matematicienilor francezi Pierre de Fermat și René Descartes. Geometria analitică îmbină algebra modernă (abstractă) cu geometria clasică. Figurile geometrice sunt definite de aceștia cu ajutorul ecuațiilor sau inecuațiilor, iar rezolvarea problemelor se face pur algebric. Apariția geometriei analitice a marcat un punct de cotitură în evoluția matematicii.
Prin introducerea unui sistem de coordonate, Fermat și Descartes au oferit o metodă prin care forme geometrice, cum ar fi curbele și suprafețele, puteau fi descrise și analizate cu ajutorul ecuațiilor algebrice.
În lucrarea sa „La Géométrie„, care face parte din „Discours de la méthode” publicată în 1637, René Descartes prezinta ideea revoluționară că pozițiile punctelor în spațiu pot fi descrise folosind numere. Pornind de la aceasta idee analizează formele geometrice folosind ecuații algebrice. Acesta a fost un pas important în dezvoltarea matematicii moderne. Lucrarea reprezintă o îmbinare între algebra, geometrie si trigonometrie, lucru care nu fusese posibil anterior.
Această abordare a deschis calea către aplicarea trigonometriei în noi moduri. Astfel sunt explorate relațiile dintre unghiuri și distanțe într-un cadru algebric. Trigonometria devine esențială în studiul proprietăților curbelor, cum ar fi elipsele, hiperbolele și parabolele. Astfel, lucrările lui Fermat și Descartes nu numai că au unit două ramuri importante ale matematicii, dar au și extins semnificativ domeniul de aplicabilitate al trigonometriei. Se facilitează astfel progresul în domenii variate, de la calculul integral și diferențial până la fizica teoretică și inginerie.
Funcțiile trigonometrice în Epoca Modernă
Numerele complexe și funcțiile trigonometrice
Abraham de Moivre, un matematician francez din secolul al XVIII-lea, care a trăit și a lucrat în mare parte în Anglia, a utilizat numerele complexe (numere de forma x+iy, unde x și y sunt numere reale și i = \sqrt[]{-1}) în expresiile trigonometrice.
Una dintre formulele sale cele mai cunoscute este formula lui de Moivre. Această formulă stabilește o legătură puternică între trigonometrie și numerele complexe. Ea este esențială în matematica superioară, în special în analiza complexă. Formula lui de Moivre afirmă că pentru orice număr real θ și orice întreg n, următoarea egalitate este adevărată:
(\cos \theta + i\sin \theta)^n = \cos(n\theta) + i\sin(n\theta)
Formula lui de Moivre permite ridicarea la putere a expresiilor trigonometrice și a numerelor complexe într-un mod elegant și simplificat. Ea facilitează calculul puterilor și extragerea rădăcinilor numerelor complexe.
Contribuția lui Leonhard Euler legătura între funcțiile trigonometrice și numerele complexe
Leonhard Euler (1707-1789) a fost unul dintre cei mai influenți matematicieni din istorie. Acesta a avut contribuții semnificative în multe domenii ale matematicii, inclusiv în trigonometrie. Lucrările sale nu numai că au extins cunoștințele existente, dar au și pus bazele pentru dezvoltărilor ulterioare în analiza matematică, teoria numerelor, mecanică și multe alte domenii.
Impactul lucrărilor lui Euler asupra trigonometriei și matematicii în general este vast. El a standardizat, de asemenea, notarea funcțiilor trigonometrice (sin, cos, tg), simplificând comunicarea ideilor matematice.
Una dintre lucrările sale cele mai influente, care a cuprins o gamă largă de subiecte matematice, inclusiv trigonometrie, este „Introductio in analysin infinitorum” (Introducere în analiza infinitelor), publicată în 1748. În această lucrare, Euler explorează funcțiile exponențiale, logaritmice și trigonometrice. În această lucrare regăsim formula lui Euler sau reprezentarea exponențială a unui număr complex:
e^{ix}=cos(x)+isin(x)unde e \approx 2.71828 este baza logaritmului natural. Aceasta reprezintă una dintre cele mai remarcabile contribuții ale sale în matematică, stabilind o legătură profundă între funcțiile trigonometrice și numerele complexe.
Înlocuind în această formula valoarea lui x cu \pi obține e^{i\pi}=cos(\pi)+isin(\pi) se obține
e^{i\pi} + 1 = 0Aceasta ecuație intrigă prin simplitatea ei și prin faptul că în ea se regăsesc atât π , e, partea imaginară i și nu în ultimul rând 1 si 0.
Alte două expresii celebre sunt obținute înlocuind θ cu –θ în Formula lui Euler:
\cos \theta = \frac{e^{i\theta} + e^{-i\theta}}{2}\\ \
\sin \theta = \frac{e^{i\theta} - e^{-i\theta}}{2i}
Prin studiile sale asupra seriilor infinite, inclusiv cele legate de e^x, sin(x), și cos(x), Leonhard Euler, a extins domeniul calculului infinitesimal. Dezvoltând teoria funcțiilor de mai multe variabile, a explorat proprietățile complexe ale funcțiilor trigonometrice. Utilizarea trigonometriei în rezolvarea problemelor geometrice complexe a demonstrat aplicabilitatea sa extinsă, influențând profund matematica și alte științe.
Funcțiile trigonometrice în Secolul al XIX-lea și al XX-lea
Dezvoltările din secolele al XIX-lea și al XX-lea în domeniul trigonometriei reflectă evoluția continuă a matematicii și a aplicabilității sale în diverse câmpuri științifice și tehnologice. În această perioadă, matematica, inclusiv trigonometria, a fost profund influențată de formalizarea conceptelor, de extinderea domeniului de aplicare și de încorporarea noilor tehnologii în cercetare și educație.
Secolul al XIX-lea
În secolul al XIX-lea, matematica a experimentat o mișcare semnificativă înspre rigurozitate și formalizare. Acest proces a influențat profund și trigonometria prin definirea mai precisă a funcțiilor trigonometrice, nu doar în contextul geometric al triunghiurilor, ci și ca funcții analitice aplicabile la argumente complexe. Pionieri precum Augustin-Louis Cauchy și Bernhard Riemann au extins domeniul funcțiilor complexe, inclusiv aspectele trigonometrice, stabilind fundamentul analizei complexe cu ajutorul formulei lui Euler ca piatră de temelie. Simultan, dezvoltarea trigonometriei sferice a marcat progrese semnificative în domenii precum astronomia, geodezia și navigația. Datorită metodelor avansate de calcul și măsurare s-a îmbunătățit acuratețea determinării pozițiilor geografice și eficientizarea cartografierii. Aceste evoluții au consolidat rolul trigonometriei ca disciplină fundamentală în avansarea științei și tehnologiei.
Secolul al XX-lea
În secolul al XX-lea, aplicarea trigonometriei în analiza matematică a cunoscut o extindere semnificativă, de la rolul său în dezvoltarea seriilor Fourier, esențiale pentru procesarea semnalelor, până la utilizarea în ecuațiile diferențiale ce descriu fenomene fizice. Aceasta a reprezentat o evoluție majoră în metodele de analiză matematică.

Emergența și evoluția informaticii au consolidat rolul trigonometriei în dezvoltarea algoritmilor pentru grafică computerizată, criptografie și analiza numerică, subliniind importanța funcțiilor trigonometrice în modelarea și manipularea spațială.
În domeniul educațional, metodele de predare a trigonometriei au beneficiat de progrese tehnologice, cu utilizarea intensivă a calculatorului grafic și a software-ului specializat, transformând modul în care trigonometria este învățată și aplicată.
Mai mult, cunoștințele trigonometrice au fost aplicate în domenii interdisciplinare: teoria relativității, mecanica cuantică sau ingineria telecomunicațiilor și economie. Acest lucru a demonstrat capacitatea sa de a modela și analiza oscilații, unde și rotații, deschizând noi orizonturi în cunoaștere și inovație.
Funcții trigonometrice aplicații în era digitală
În era digitală, trigonometria joacă un rol esențial într-o varietate de aplicații avansate. Printre acestea se regăsesc grafica computerizată, procesarea semnalelor digitale, criptografia, navigația prin satelit și realitatea augmentată.

Funcțiile trigonometrice sunt fundamentale în modelarea și reprezentarea spațiilor tridimensionale în jocurile video și în animații. Permit calculul precis al pozițiilor și traiectoriilor în sistemele GPS. Facilitează conversia între formatele de timp și frecvență în procesarea semnalelor audio și video. Trigonometria este aplicată în dezvoltarea algoritmilor de criptare, pentru securizarea comunicațiilor digitale și în tehnologiile de realitate virtuală și augmentată. Prin urmare, cunoașterea și aplicarea trigonometriei rămân vitale pentru avansarea tehnologică și inovația necesare în era digitală.
Concluzie
Istoria funcțiilor trigonometrice dezvăluie un drum fascinant al schimbului de cunoștințe matematice între diverse culturi de-a lungul timpului. Începând cu inovațiile babilonienilor, pe care le regăsim astăzi în orice moment când citim ceasul, și continuând cu contribuțiile civilizațiilor grecești, indiene, arabe și până la cercetătorii din epoca modernă, aceste funcții au fost baza progresului în știință și tehnologie. Fiecare etapă în dezvoltarea trigonometriei a fost marcată de o transformare profundă a ideilor, pe măsură ce acestea erau adoptate și adaptate de diferite culturi. Această încrucișare culturală a îmbogățit matematica, ducând la noi descoperiri și metode. Astfel, trigonometria reprezintă și o mărturie a dialogului continuu între civilizații în căutarea înțelegerii universului.
Referințe:
History of trigonometry
Histoire des fonctions trigonométriques
Plimpton 322 is Babylonian exact sexagesimal trigonometry
Muhammad ben Jaber ben Sinan Al-Battani
The Beginnings of Trigonometry
Unele imagini sunt generate cu ChatGPT



