Modulul unui număr real – 17 proprietăți fundamentale

Modulul unui număr real este distanța absolută a acelui număr față de zero (originea) pe axa numerelor reale. Putem considera de altfel că este numărul real luat fără semn.

Modulul unui număr real sau valoarea absolută a unui număr real x, este notat |x|. Această notație pentru valoarea absolută a fost introdusă in secolul al XIX-lea de către Karl Weierstrass o dată ce conceptul de modul a fost formalizat și introdus în matematică.

Definiție:

|x| = \left\{
	  \begin{array}{ll}
	  -x \, , x < 0 \\
	   \ \ \  0 \, , x =0 \\
            \ \ \ x \, , x >0 \\
	  \end{array}
  \right.

După cum se poate observa din aceasta definiție valoarea absolută a lui x este întotdeauna un număr pozitiv sau zero, niciodată negativ.

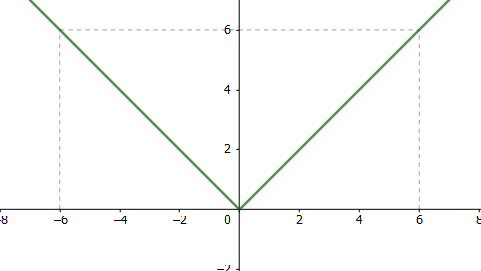
Modulul și proprietățile sale

Modulul unui număr real are mai multe proprietăți importante, care sunt esențiale în rezolvarea problemelor. Iată câteva dintre acestea:

(\forall)x, y  \in \R \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \\\;\\
\textbf{1. } |x| ≥ 0 \qquad \qquad \qquad \qquad \ \\\\\;\\
\textbf{2. } |x| =0 \Leftrightarrow  x =0 \qquad \ \ \ \ \ \ \  \ \ \ \\\ \;\\ \ 
\textbf{3. } |-x| =|x|  \qquad \qquad \qquad \ \ \ \ \\\;\\
\textbf{4. } |x| =|y|  \Leftrightarrow \left\{
	  \begin{array}{ll}
	  x = y  \\ 
\text{sau}\\
	   x = -y
	  \end{array}
  \right. \ \ \ \ \  \\\;\\
\textbf{5. } |x\cdot y| =|x|\cdot |y|\qquad \qquad  \ \ \ \ \\\;\\
\textbf{6. } \bigg|\dfrac{x}{y}\bigg| =\dfrac{|x|}{|y|}, \ y \neq0 \qquad \qquad  \ \ \ \ 

\textbf{7. } -|x| \leq x \leq|x|\qquad \qquad  \ \ \ \ \\\;\\
\textbf{8. } |x -y|  = | y -x| \qquad \ \ \ \  \ \ \ \ \\\;\\
\textbf{9. } |x + y| \leq |x| + |y| \qquad \ \ \ \  \ \ \ \ \\\;\\
\textbf{10. } |x -y| \leq |x| + |y| \qquad \ \ \ \  \ \ \ \ \\\;\\
\textbf{11. } ||x| -|y|| \leq |x-y| \qquad \ \ \ \  \ \ \ \ \\\;\\
\textbf{12. } ||x| -|y||  \leq |x+y|\leq |x| + |y| \qquad  \\\;\\

\textbf{13. } |x|^2 = x^2  \qquad \ \ \ \  \ \ \ \ \\\;\\
\textbf{14. } \sqrt[2n]{x^{2n}} = |x|  \implies  \sqrt[]{x^{2}} = |x|\\\;\\
\text{dar  } \sqrt[2n+1]{x^{2n+1}} = x

Modulul: Ecuații fundamentale

|x - a| = b; \ \ a, \ b \in \R \\ \;\\
\begin{array}{|r|c| } \hline 
b  \qquad  & \text{Mulțimea soluțiilor}\\ \hline
b  \lt 0   & \emptyset\ \\ \hline
b  = 0   & \left\{ a \right\}\ \\ \hline
b   \gt 0   & \left\{ a-b \  \ ;  \ \ a + b \right\}\ \\ \hline
\end{array}

Observăm că dacă b < 0 ecuația nu are soluții reale. Acest lucru se datorează faptului că modulul unei expresii este întotdeauna pozitiv, deci un număr negativ nu poate fi soluție validă.
Rămân de analizat două cazuri cand b = 0 sau b > 0.

Dacă b = 0 atunci ecuația | x – a | = b are o soluție obținută aplicând definiția modulului:
x - a = 0 => x = a

Dacă b > 0 atunci ecuația | x – a | = b are două soluții obținute aplicând definiția modulului:
x - a = b => x = a + b
x - a = -b => x = a - b

Caz particular a=0

\text{fie } b \in \R \text { a. î. }
|x| = b \implies\\ \;\\  \implies  \left\{
	  \begin{array}{ll}
	   b < 0 \implies  \text{ecuația nu are soluții} \\
	  b =0 \implies x =0 \\
            b > 0 , \implies x \in  \left\{-b, b\right\}
	  \end{array}
  \right.

Modulul: Inecuații fundamentale

Inegalitatea cu modul și semnul strict mai mare

|x - a| > b; \ \ a, \ b \in \R \\ \;\\
\begin{array}{|r|c| } \hline 
b  & \text{Mulțimea soluțiilor}\\ \hline
b  \lt 0 & \R\ \\ \hline
b  = 0 & \R\setminus \left\{ a \right\}\ \\ \hline
b   \gt 0 &   (- \infty,\ a-b) \cup	 (a+b, \ + \infty) \\ \hline
\end{array}

Observăm că dacă b < 0 inecuația are o infinitate de soluții reale. Acest lucru se datorează faptului că modulul unei expresii este întotdeauna pozitiv, deci mai mare decât orice număr negativ.
Rămân de analizat două cazuri cand b = 0 sau b > 0 in ambele cazuri distanta dintre x si a trebuie să fie strict mai mare decât b astfel soluția va fi reprezentată de două intervale disjuncte obținute aplicând definiția modulului:
x - a > b sau
-x + a > b de unde obținem x > a + b sau x < a - b

Caz particular a = 0

(\forall) b \in\R_+ \ ,|x| \geq b\Leftrightarrow   -x \in (- \infty,-b] \cup	 [b, + \infty)

Inegalitatea cu modul și semnul strict mai mic

|x - a| < b; \ \ a, \ b \in \R \\ \;\\
\begin{array}{|r|c| } \hline 
b  & \text{Mulțimea soluțiilor}\\ \hline
b  \lt 0 &  \emptyset\ \\ \hline
b  = 0 &  \emptyset\ \\ \hline
b   \gt 0 &   (a-b\ , \ a+b) \\ \hline
\end{array}

Observăm că dacă b < 0 sau b = 0 inecuația nu are nicio soluție sau soluția este mulțimea vidă. Acest lucru se datorează faptului că modulul unei expresii este întotdeauna pozitiv, deci mai mare decât orice număr negativ.
Rămâne de analizat doar cazul când b > 0. Aceasta inegalitate indică faptul că distanța dintre x si a trebuie să fie strict mai mică decât b. Astfel soluția va fi reprezentată de un interval deschis obținut aplicând definiția modulului:
x - a < b sau
-x + a < b de unde obținem x < a + b sau x > a - b

Caz particular a = 0

(\forall) b \in\R_+ \ ,|x| \leq b\Leftrightarrow   x \in [-b, \ b] 

Mai multe inegalități referitoare la modul găsești și pe pagina noastră cu inegalități importante.