Problema rezolvată #24 – ONGM 2020-2021

Problemă rezolvată dintre subiectele propuse pentru clasa a X-a la ONGM 2020-2021.

Dacă ABC este un triunghi dreptunghic în A, atunci folosind notațiile uzuale suma b+c este egală cu:

\textbf{A. } r + R \ \ \ \ \ \textbf{B. } \dfrac{r+R}{2} \ \ \ \ \ \ \textbf{C. } 2(r + R) \\\;\\ \qquad\textbf{D. } \dfrac{r+R}{r\cdot R} \qquad \textbf{E. } a + r + R

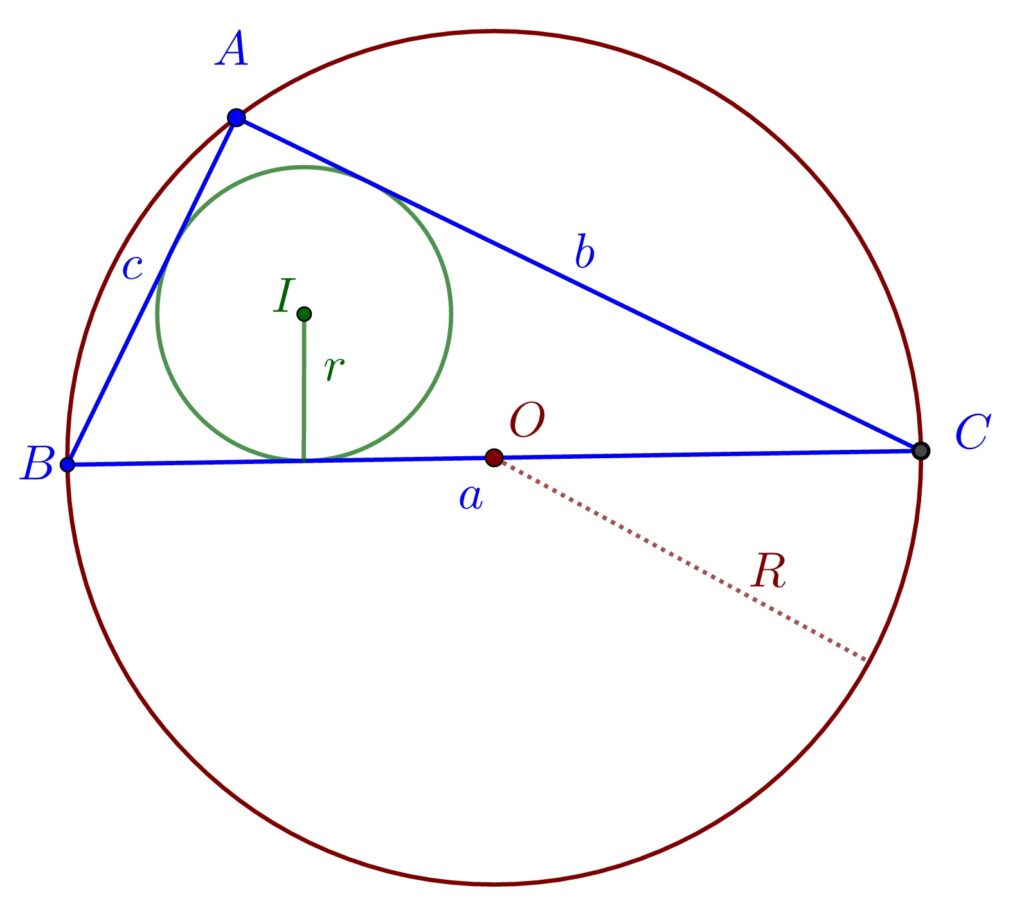
Suprafața triunghiului poate fi exprimată în funcție de raza cercului înscris și semiperimetru astfel:

\left. \begin{array}{ll}S = r \cdot p \\\;\\ S = \dfrac{bc}{2}\\\;\\ p = \dfrac{a+b+c}{2} \end{array} \right \} \implies \\\;\\ \implies \dfrac{bc}{2} = r \cdot \dfrac{a+b+c}{2} \implies \\\;\\ \implies bc = r \cdot (a + b+c) \\ \;\\ \left. \begin{array}{ll} b^2 + 2bc + c^2 = (b+c)^2 \\\;\\ b^2 + c^2 = a^2 \text{(Th. Pitagora)} \end{array} \right \}\implies \\ \;\\\implies (b+c)^2 = a^2 + 2bc \implies \\\;\\ \left. \begin{array}{ll} \implies bc = \dfrac{(b+c)^2 - a^2}{2} \\\;\\ \qquad \ \ bc = r \cdot (a + b+c)\\\;\\ \qquad \ \ a =2R \end{array} \right \} \implies \\\;\\ \implies \dfrac{(b+c)^2 - (2R)^2}{2} = r \cdot (2R+b+c) \implies \\\;\\ \implies \dfrac{\cancel{(b+c+2R)}(b+c - 2R)}{2} = \\ \ \\ =r \cdot\cancel{(2R+b+c)} \implies \\\;\\ \implies \dfrac{(b+c-2R)}{2} = r \implies \\\;\\ \implies b+c = 2 r + 2R \implies \\\;\\ \implies b+c =2\cdot (r+R)

Răspunsul este C, 2(r + R).

Pe aceeași temă


Chris Waring	Stephen Hawking
De la 0 la infinit in 26 de secole...	Universul într-o coajă de nucă
cartepedia.ro	cartepedia.ro

Jordan Ellenberg	Daniel Kahneman
Cum să nu greșești	Gândire rapidă, gândire lentă
cartepedia.ro	cartepedia.ro

Pe aceeași temă