Problemă rezolvată #42 – geometrie problemă cu romb

În triunghiul ABC dreptunghic în A fie G intersecția înălțimii AD, D \in (BC) , cu bisectoarea [BE, E \in (AC) și fie EF \perp BC, \space F\in (BC) . Demonstrați că AEFG romb.

Această problemă a fost publicata in grupul MATEMATICA ONLINE.

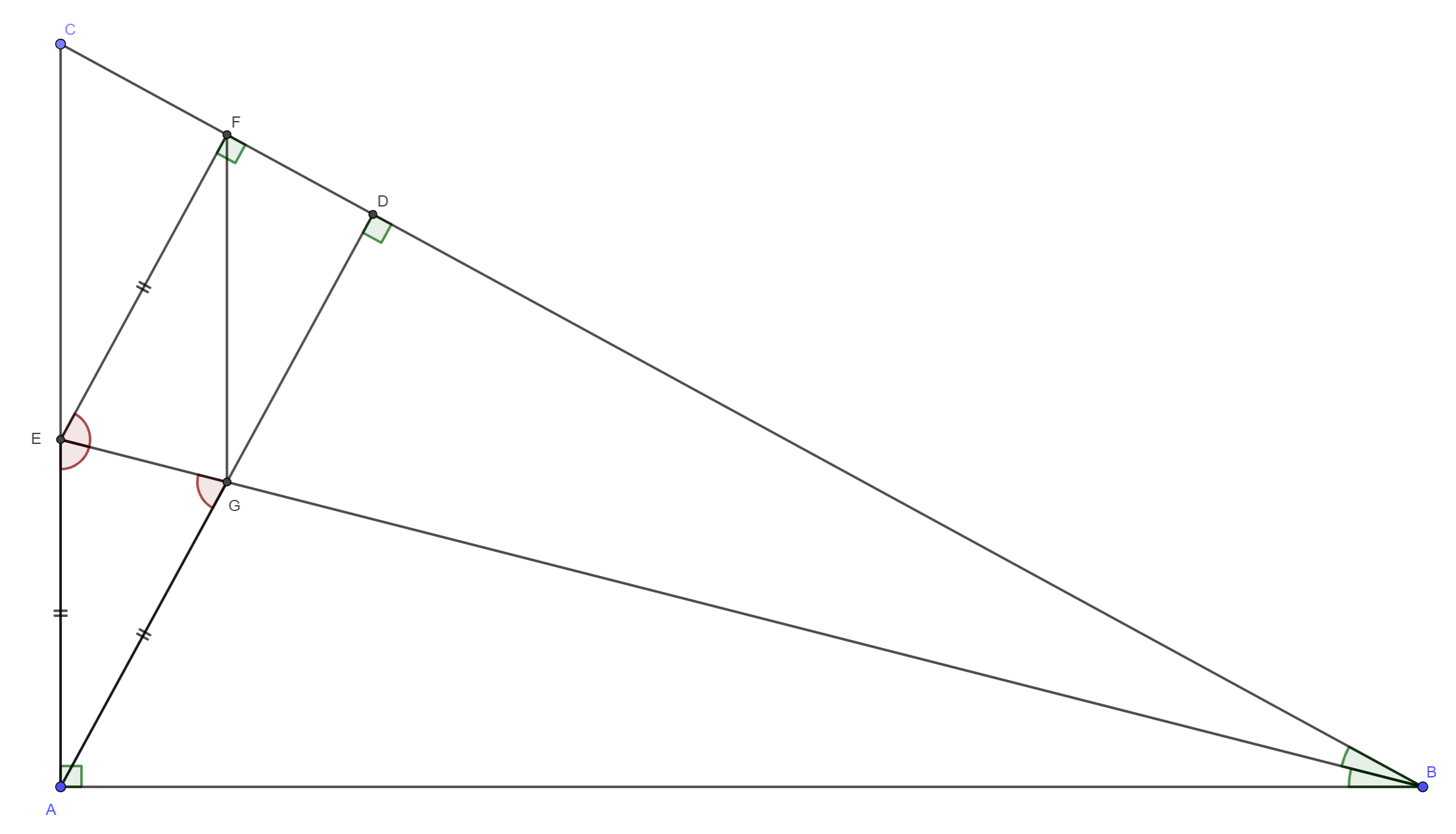
Vom construi figura geometrică conform enunțului:

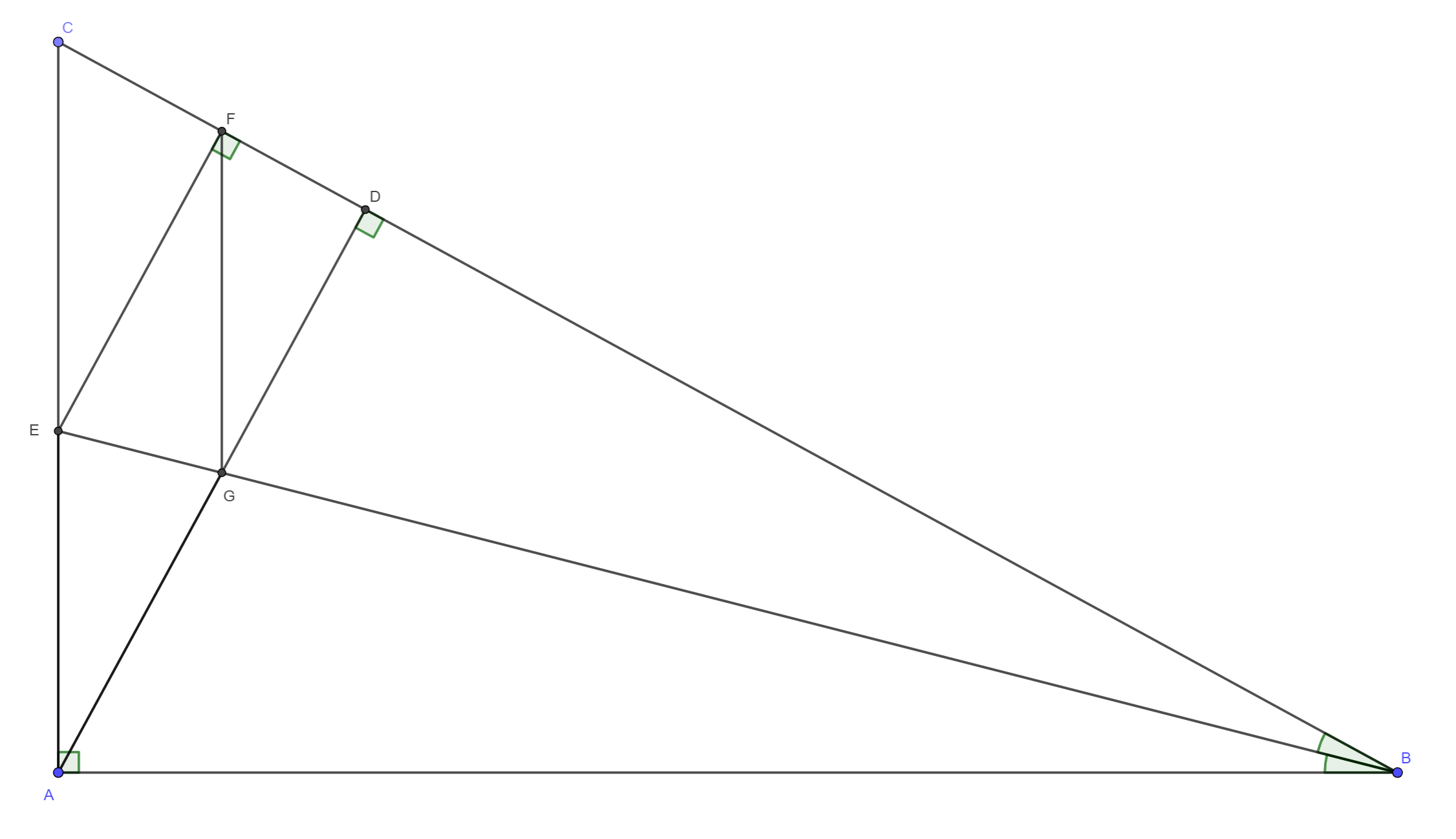
Pentru demonstrarea acestei probleme ne vom folosi de faptul că două drepte perpendiculare pe aceeași dreaptă sunt paralele. Deci EF || AD deoarece ambele sunt perpendiculare pe BC.

Știm de asemenea ca dacă două drepte sunt paralele, atunci ele formează cu orice secantă perechi de unghiuri alterne interne. Vom considera dreptele paralele EF || AD și EG secantă ceea ce face ca unghiurile alterne interne \measuredangle{FEG} \equiv \measuredangle{EGA} să fie congruente.

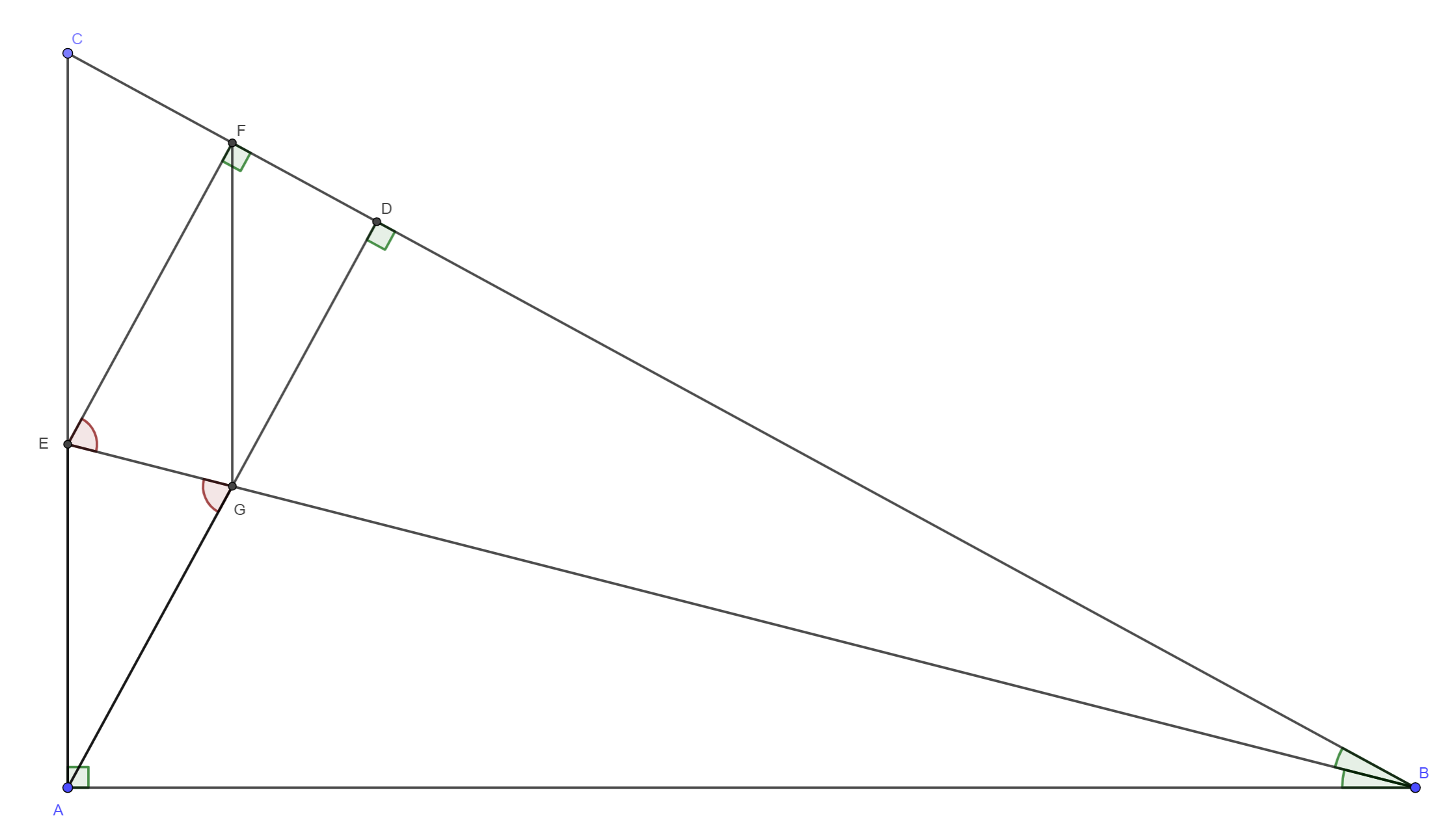
Vom folosi în continuare de faptul că daca luăm orice punct de pe bisectoarea unui unghi, atunci distanțele de la acest punct la laturile unghiului sunt egale. (Știm că distanța de la un punct la o dreaptă este lungimea segmentului care se întinde din acel punct până la piciorul perpendicularei pe dreaptă dusă din acel punct). Ceea ce face ca AE să fie egal cu EF.

\begin{rcases}
   AE \perp AB \\
  EF \perp BC\\
 E \in EB \\
  EB  \space \text{bisectoarea unghiului } ABC
\end{rcases}\xRightarrow{} \\[1em] 

AE \equiv EF

Vom demonstra în continuare că triunghiul AGE este isoscel. Pentru aceasta vom arăta mai întâi că triunghiurile EAB si EFB sunt congruente.

\begin{rcases}
   AE \equiv EF \\
  EB  \space \text{ipotenuză}
\end{rcases}\xRightarrow{IC} \\[2em]

\vartriangle EAB \equiv \vartriangle EFB \implies \\[2em]

\begin{cases}
 \measuredangle{AEG} \equiv \measuredangle{FEG}  \\
   AE \equiv EF
\end{cases}

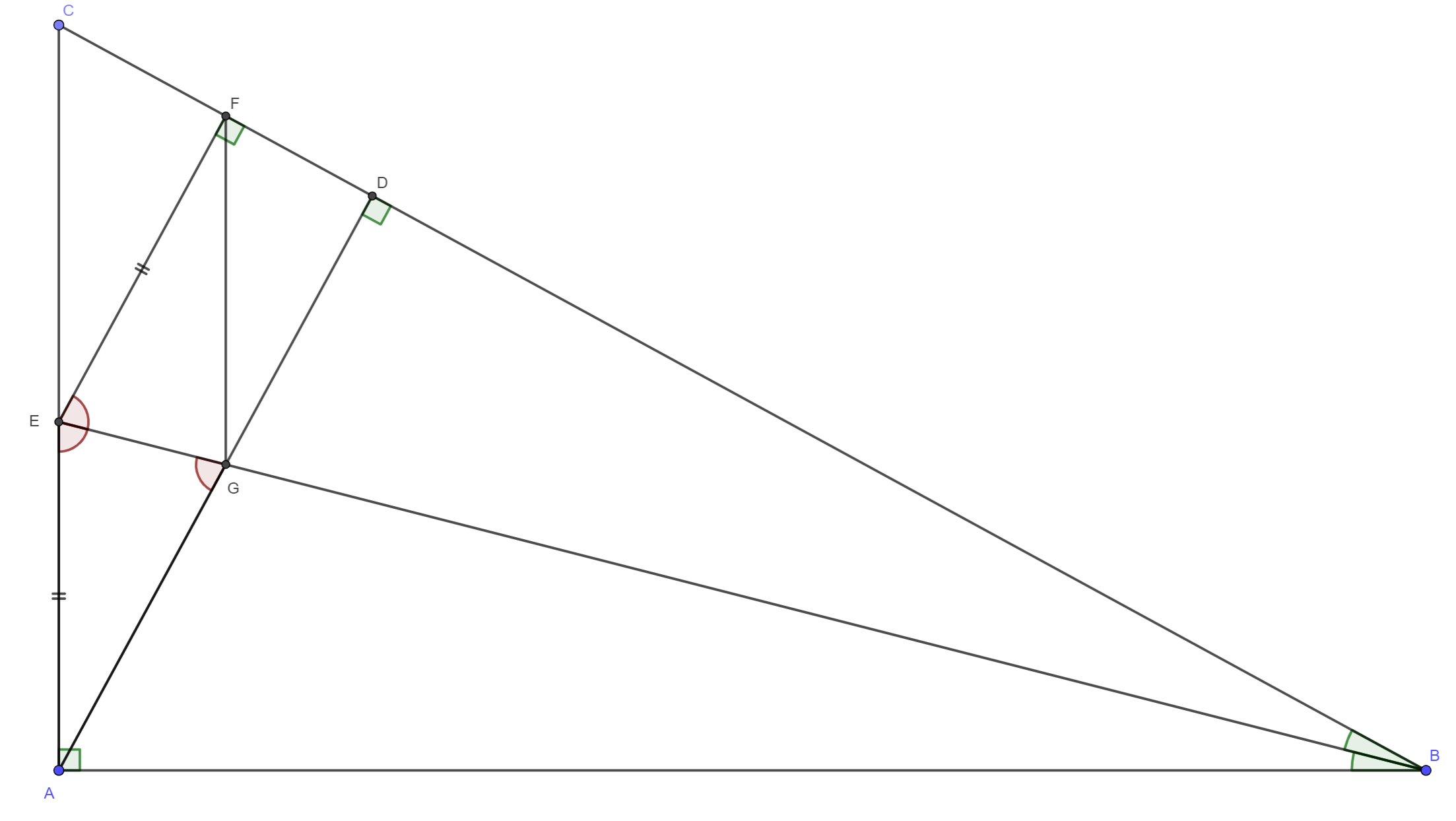
Însă mai devreme am demonstrat că \measuredangle{FEG} \equiv \measuredangle{EGA} ceea ce face ca \measuredangle{AEG} \equiv \measuredangle{EGA} deci triunghiul AGE este isoscel.

\begin{rcases}

\measuredangle{FEG} \equiv \measuredangle{EGA} \\[1em]
\measuredangle{FEG} \equiv \measuredangle{GEA} 
  
\end{rcases} \implies \\[1em]

\measuredangle{AEG} \equiv \measuredangle{EGA}\implies\\[1em]
\vartriangle{EAG} \space \text{isoscel}\implies \\[1em] 

EA \equiv AG

Dar EF || AG am stabilit acest lucru mai devreme și am arătat că sunt congruente. Din definiția paralelogramului știm că orice patrulater convex în care două dintre laturi sunt paralele și congruente este paralelogram. Ceea ce face ca AGFE să fie paralelogram.

\begin{rcases}

 EF \parallel AG  \\[1em]
EF \equiv AG 
  
\end{rcases} \implies \\[1em]

\text {patrulaterul EFGA  este paralelogram}

Am demonstrat mai devreme că \measuredangle{AEG} \equiv \measuredangle{FEG} . Ceea ce face ca EG sa fie bisectoarea unghiului AEF. Din proprietățile rombului știm că orice paralelogram în care o diagonală este bisectoare pentru unghiurile acestuia este romb.

\begin{rcases}
\text {EFGA  paralelogram} \\[1em]

 \measuredangle{AEG} \equiv \measuredangle{FEG} \\[1em]
\text {EG  diagonală } \\[1em]
  
\end{rcases} \implies \\[1em]

\text {patrulaterul EFGA  este romb}