Teorema lui Napoleon

Fie un triunghi oarecare ABC. Teorema lui Napoleon spune că centrele triunghiurilor echilaterale construite pe laturile acestuia formează un triunghi echilateral. În figura de mai jos, am luat punctele A, B și C la întâmplare (dar nu colineare). Apoi, am construit triunghiurile ACK, CBH și ABG echilaterale, pe laturile triunghiului ABC.

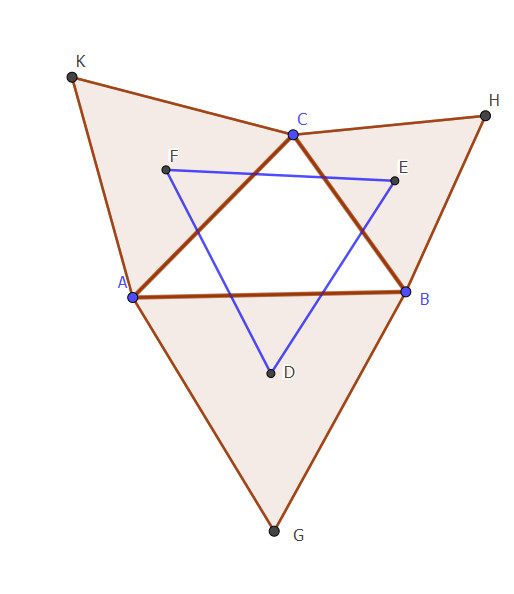
Fie punctele F, E și D centrele acestor triunghiuri. Știm că într-un triunghi echilateral ortocentrul și centrele cercurilor înscris și circumscris triunghiului coincid. Triunghiul DEF este, conform acestei teoreme, echilateral.

Puțină istorie

Această teoremă este atribuită împăratului francez, Napoleon Bonaparte (1769-1821), deși nu este foarte sigur că el ar fi cel care a descoperit-o ^[1]. O descriere timpurie a problemei apare în almanahul The Ladies’ Diary în anul 1825, la patru ani după moartea împăratului, ca o întrebare adresată de matematicianul englez William Rutherford, iar în anul 1826 apar în aceeași revistă și două metode de demonstrație, pe care le vom prezenta și noi mai departe^[2]. Prima se bazează pe asemănarea triunghiurilor; a doua presupune calculul laturilor triunghiului DEF în funcție de dimensiunile triunghiului ABC, fiind relativ mai ușor de urmărit.

Prima mențiune a numelui lui Napoleon în acest context apare într-o enciclopedie din anul 1867, iar mai apoi în ediția 1911 a lucrării Elementi di Geometria, Aureliano Faifofer.

Metoda I – triunghiuri asemenea

Pentru început, construim segmentele AH și BK și arătăm că acestea sunt congruente. Mai apoi, arătăm că triunghiurile DBE și ABH sunt asemenea, la fel și AFD și AKB. Din rapoartele între laturile acestor triunghiuri va rezulta că segmentul DF este congruent cu DE.

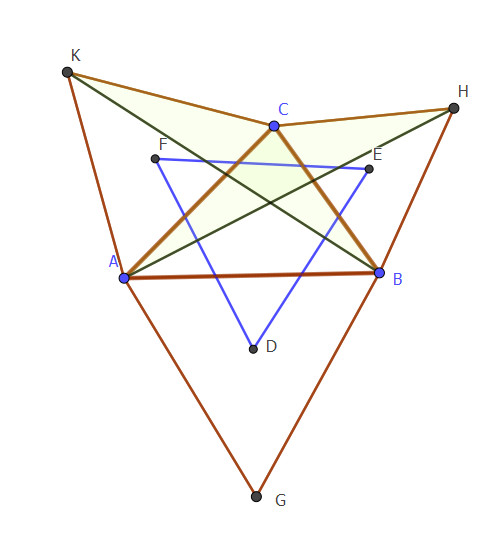
\begin{rcases} \triangle BCH\text{ ech.} \implies BC\equiv CH\\
\triangle ACK\text{ ech.} \implies CK \equiv AC \\
\angle BCK \equiv\angle ACH 
\end{rcases} \implies\\[1em]
\triangle BCK\equiv\triangle ACH\implies\\[1em]

 

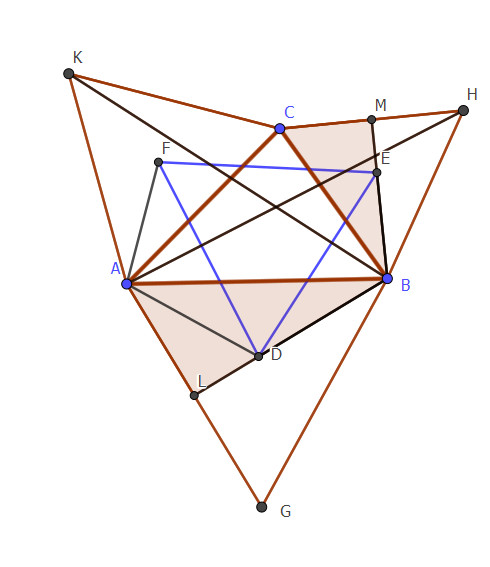
\begin{equation}AH\equiv BK \end{equation} 

Ducem înălțimile din vârful B pentru triunghiurile BCH și ABG, obținând segmentele BM și, respectiv, BL. Observăm că triunghiurile BLA și BMC sunt asemenea.

\begin{rcases}
m(\measuredangle ABL) = m(\measuredangle MBC) = 30\degree\\[1em]
m(\measuredangle BLA) = m(\measuredangle BMC) = 90\degree
\end{rcases} \implies\\[1em]

\begin{equation}\implies \triangle BLA \sim\triangle BMC\end{equation}

\begin{equation}\implies \frac{BL}{BM}=\frac{AB}{BC}=\frac{AL}{CM}\end{equation}

Cum punctele D și E sunt centre de greutate în triunghiurile BGA și, respectiv, BHC, înseamnă că ele se află la două treimi din înălțimile BL, respectiv BM, de vârful B.

\frac{BD}{BE}=\frac{\displaystyle  \frac{2}{3}BL}{\displaystyle \frac{2}{3}BM}\implies\\[1em]

\begin{equation}\implies \frac{BD}{BE}=\frac{BL}{BM}\end{equation}

Ne aducem aminte, urmărim să demonstrăm că triunghiurile DBE și ABH sunt asemenea, iar relațiile (3) și (4) ne ajută în acest scop.

Vom folosi cazul de asemănarea LUL, observând că unghiurile DBE și ABH sunt amândouă egale cu 60\degree + \angle ABC

\displaystyle\frac{BD}{BE} = \frac{AB}{BC} \implies\\[1em]
\begin{rcases} \implies \displaystyle\frac{BD}{AB}= \displaystyle\frac{BE}{BC}\\[1em] \displaystyle BC\equiv BH\end{rcases}\implies\\[1em]
\begin{rcases}\implies\displaystyle\frac{BD}{AB}=\frac{BE}{BH}\\[1em]m(\measuredangle DBE)=m(\measuredangle ABH) \end{rcases}\overset{LUL}{\implies}\\[1em]

 \begin{equation}\implies
\triangle DBE \sim\triangle ABH\end{equation}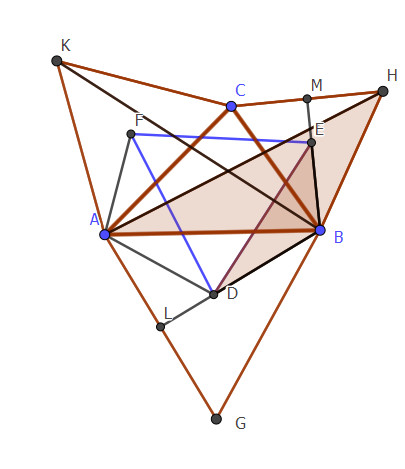

Din (5), rezultă egalitatea:

\begin{equation}\displaystyle \frac{BD}{AB} = \frac{BE}{BH} = \frac{DE}{AH}\end{equation}

În mod asemănător, demonstrăm și că triunghiurile AFD și ABK sunt asemenea.

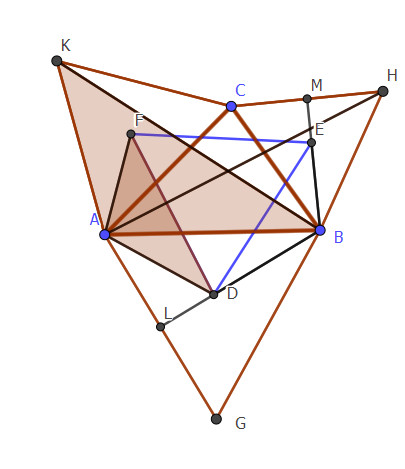
Vom vedea acum și de ce a trebuit să demonstrăm relația (1), congruența segmentelor BK și AH. Ținând cont că D este centrul cercului circumscris triunghiului ABG, AD și BD sunt raze în acest cerc. Atunci:

\begin{rcases}\displaystyle \frac{AD}{AB} = \displaystyle\frac{AF}{AK}= \displaystyle\frac{DF}{BK} \\[1em] 
\displaystyle AD\equiv BD
\end{rcases}\implies\\[1em]
\begin{rcases}\implies \displaystyle \frac{BD}{AB} = \displaystyle\frac{AF}{AK} =\displaystyle\frac{DF}{BK}\\[1em]
(6)\implies  \displaystyle \frac{BD}{AB}=\displaystyle\frac{DE}{AH}
\end{rcases}\implies\\[1em]
\begin{rcases}\implies\displaystyle \frac{DE}{AH}= \displaystyle\frac{DF}{BK}\\[1em]
(1) AH \equiv BK
\end{rcases}\implies \\[1em]
\implies \boxed{DE\equiv DF}

Analog, se poate demonstra și că \displaystyle DF\equiv EF, deci \displaystyle \triangle DEF este echilateral.

Metoda II – calculul laturilor

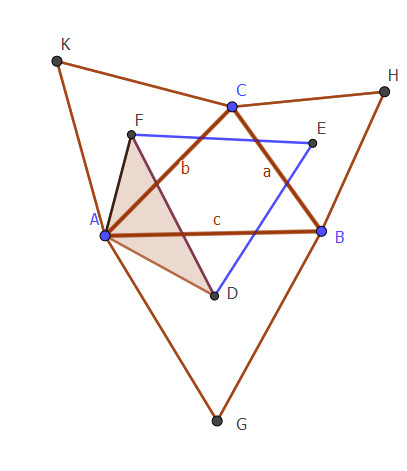
Considerăm a lungimea segmentului BC, b lungimea segmentului AC și c lungimea segmentului AB. Putem calcula dimensiunea segmentului DF aplicând teorema lui Pitagora generalizată în triunghiul AFD.

 \begin{equation}\begin{split}&DF^2 = AF^2 + AD^2-\\&-2\cdot AF\cdot AD\cdot cos(\angle{FAD})\end{split}\end{equation}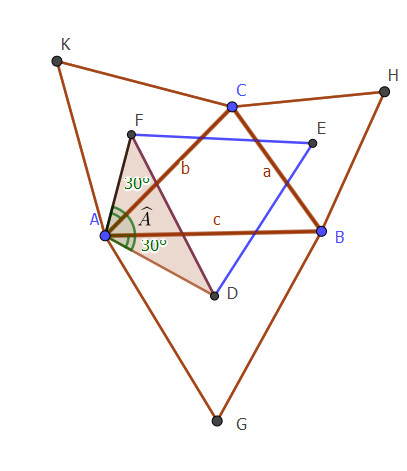

Unghiurile CAF și BAD au fiecare câte 30 de grade, AF și AD fiind bisectoare în triunghiuri echilaterale. Notând cu \widehat{A} unghiul CAB din triunghiul ABC rezultă că:

cos(\angle FAD) = cos(\widehat{A}+60\degree)=\\[1em]
=cos(\widehat{A})cos(60\degree) -sin(\widehat{A})sin(60\degree)  \\[1em]
  

\begin{equation}=\frac{1}{2}cos(\widehat{A})-\frac{\sqrt{3}}{2}sin(\widehat{A})\end{equation}

Pe cos(\widehat{A}) îl aflăm din teorema lui Pitagora generalizată în triunghiul ABC:

a^2=b^2+c^2-2bc\cdot cos(\widehat{A})\\[1em]

\begin{equation}cos(\widehat{A})= \frac{b^2+c^2-a^2}{2bc}\end{equation}

Pe sin(A) îl putem afla din formulele de calcul pentru aria triunghiului, notând cu S aria triunghiului ABC.

S = \frac{1}{2}bc\cdot sin(\widehat{A}) \implies \\[1em]

\begin{equation}sin(\widehat{A}) = 2\frac{S}{bc}\end{equation}

Înlocuim relațiile (9) și (10) în egalitatea (8) și obținem:

cos(\angle FAD) =\frac{b^2+c^2-a^2}{4bc}-\frac{S\sqrt{3}}{bc} \\[1em]

cos(\angle FAD)=\frac{b^2+c^2-a^2-4S\sqrt{3}}{4bc}\\[1em]\begin{equation}\\\end{equation}

FA și AD sunt relativ ușor de exprimat în funcție de a, b și c – ne aducem aminte, acest lucru ne trebuia pentru a-l exprima pe DF în funcție de laturile triunghiului ABC, în relația (7).

FA este \displaystyle \frac{2}{3} din înălțimea unui triunghi echilateral cu latura b.

\begin{equation}\begin{split} FA=\frac{\cancel2}{3}\frac{\sqrt{3}}{\cancel2}b=\frac{b}{\sqrt{3}}\\[1em]AD=\frac{c}{\sqrt{3}}\end{split}\end{equation}

Înlocuim (11) și (12) în relația (7) și obținem:

\begin{split}&DF^2 = AF^2 + AD^2-\\&-2\cdot AF\cdot AD\cdot cos(\angle{FAD})\end{split}\\[2em]
\begin{split}&DF^2 = \frac{b^2}{3}+\frac{c^2}{3}-\\[1em]&-\frac{\cancel{2bc}}{3}\frac{b^2+c^2-a^2-4S\sqrt{3}}{\cancel{4bc}}\end{split} \\[2em]
\begin{split}&DF^2=\frac{b^2+c^2}{3}-\\&-\frac{b^2+c^2-a^2-4S\sqrt{3}}{6}\end{split} \\[2em]

\boxed{\begin{split}DF^2=\frac{a^2+b^2+c^2+4S\sqrt{3}}{6}\end{split}}\begin{equation}\\\end{equation}

Se observă că relația (13) nu depinde în nici un fel de latura triunghiului DEF pe care o calculăm, ci numai de dimensiunile laturilor triunghiului ABC și de aria acestuia. Vom obține deci aceeași valoare și pentru celelalte laturi, DE și EF. În concluzie, triunghiul DEF este echilateral.