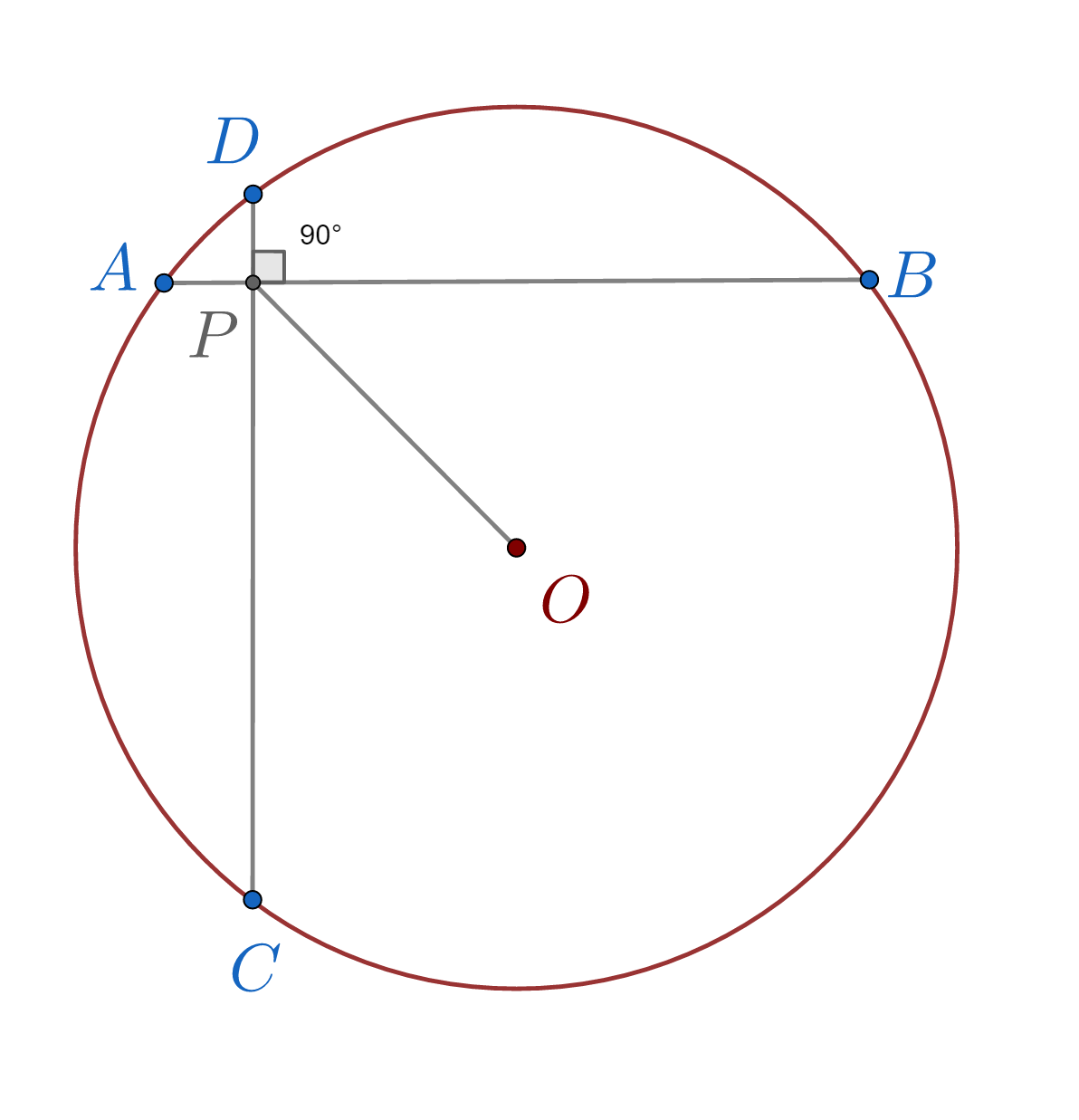
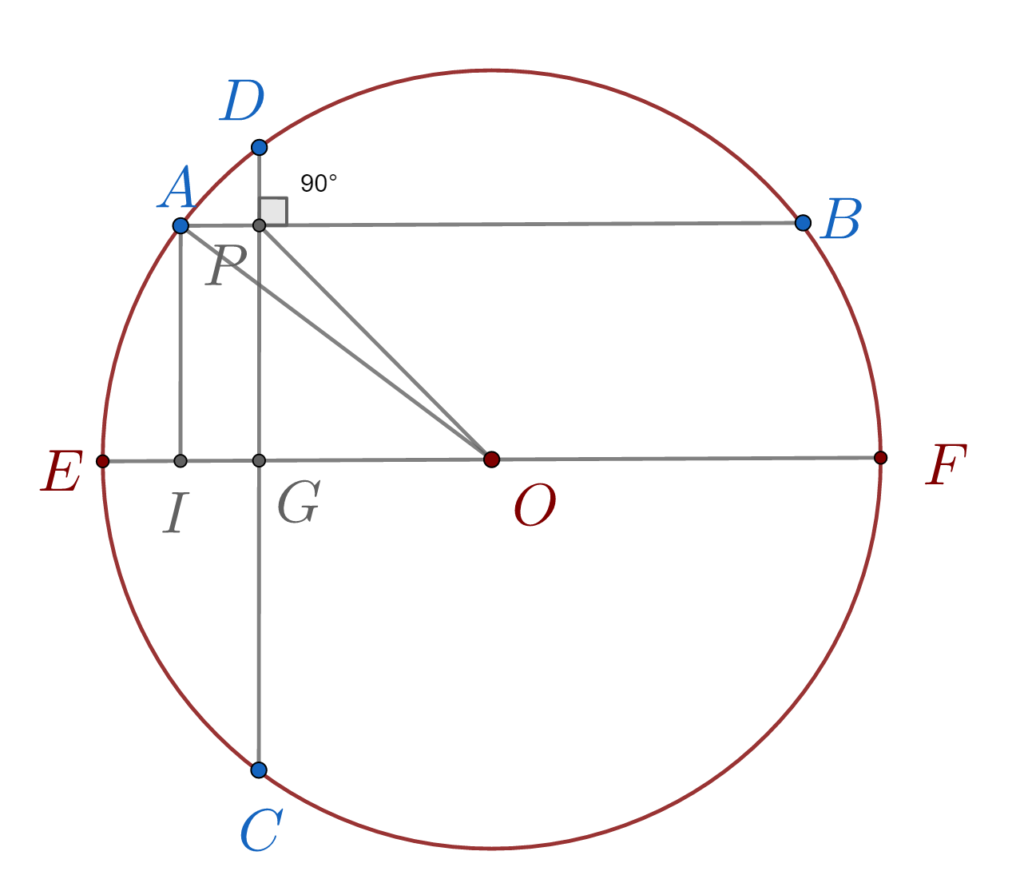
În figura de mai jos sunt desenate două coarde perpendiculare AB=CD =8cm, în cercul cu centrul în O și raza de 5cm. Dacă P este punctul comun al celor două coarde, să se afle lungimea segmentului OP.
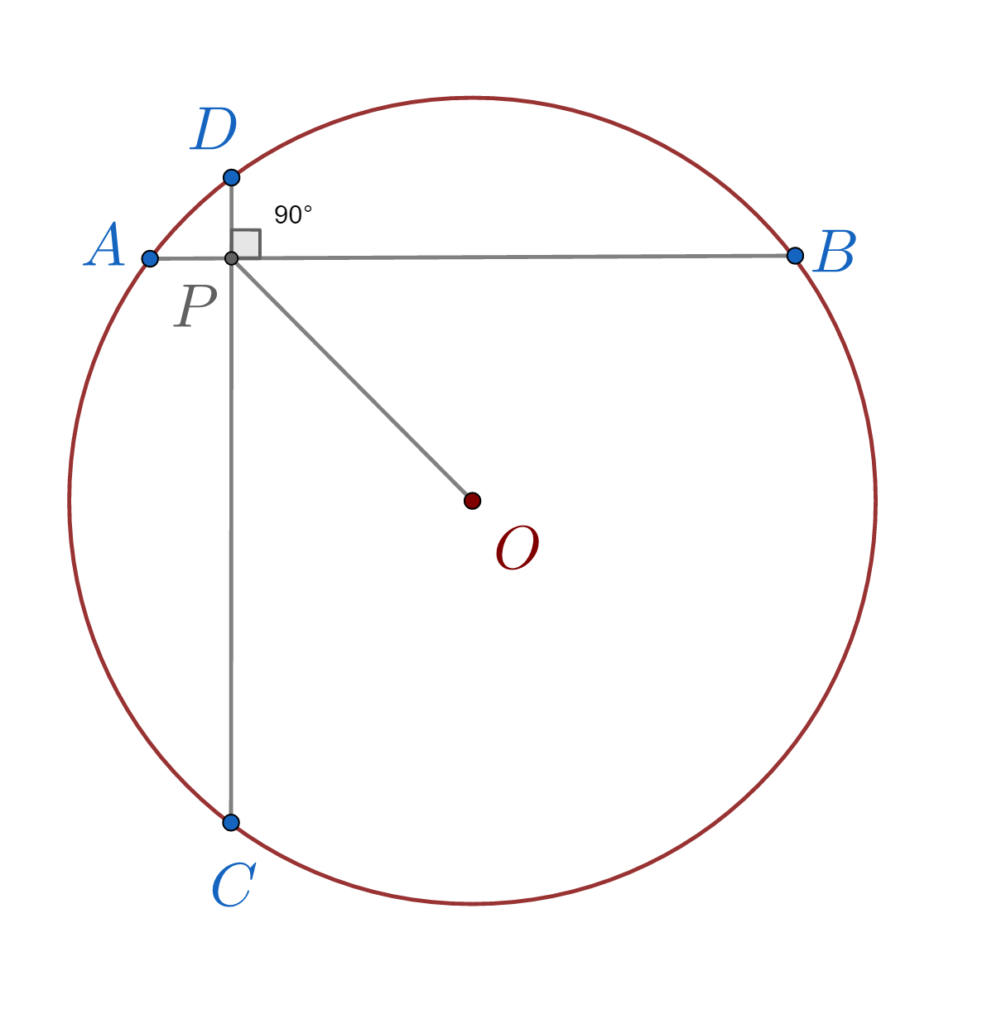
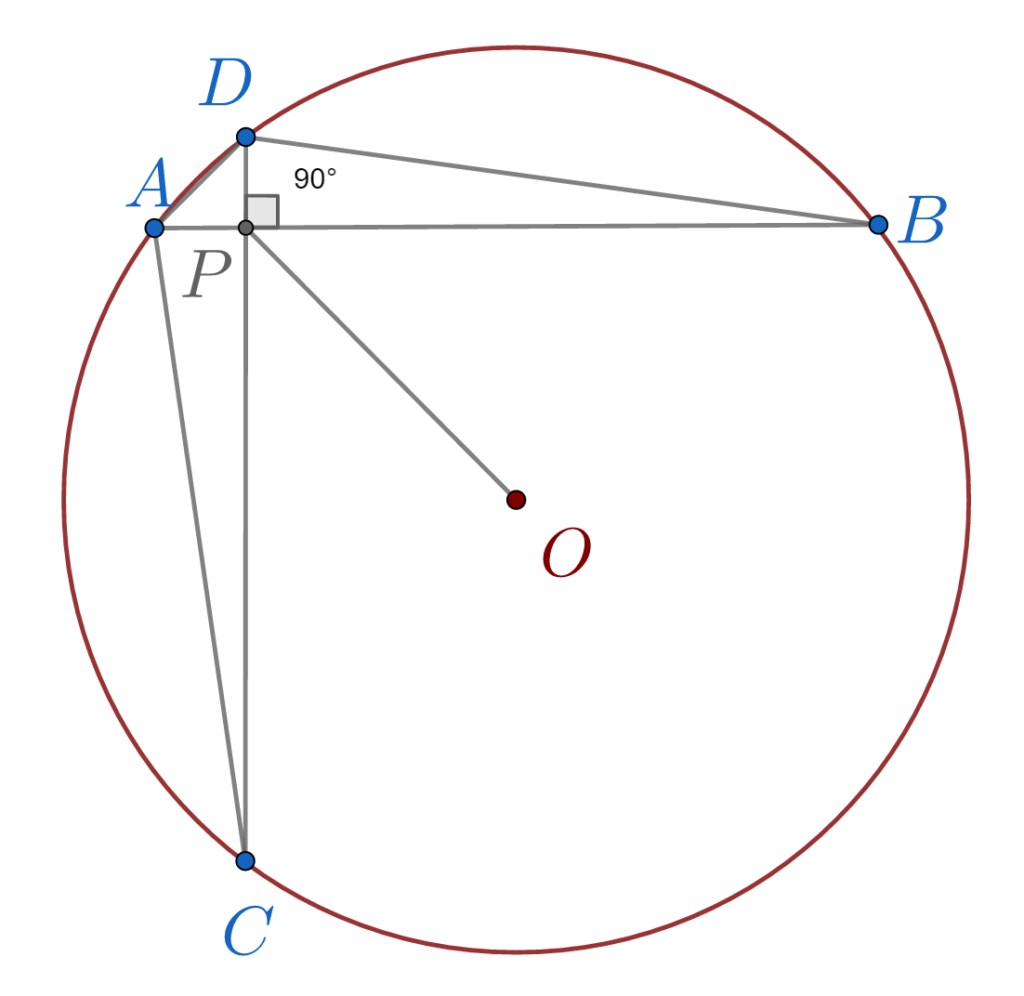
Demonstrăm mai întâi că AP este egal cu PD. Unghiurile ACD și ABD subîntind același arc de cerc deci sunt egale. Arătăm și că arcul AC este egal cu arcul BD. Știind că la arce egale se opun coarde egale, avem că AC este egal cu BD. De aici vom obține ca AP este egal cu PD.
\left.
\begin{array}{ll}
m(\measuredangle ACD) = \frac{\overset{\frown}{AD}}{2}\\\;\\
m(\measuredangle ABD) = \frac{\overset{\frown}{AD}}{2}
\end{array}
\right \} \implies \\\;\\\implies m(\measuredangle ACD) =m(\measuredangle ABD)
\\\;\\
\left.
\begin{array}{ll}
CD = AB \implies \overset{\frown}{CD} = \overset{\frown}{AB}\\
\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\overset{\frown}{CD} = \overset{\frown}{AC}+ \overset{\frown}{AD}\\
\;\;\;\;\;\;\;\;\;\;\;\;\;\;\ \overset{\frown}{AB} =\overset{\frown}{BD}+ \overset{\frown}{AD}\\
\end{array}
\right \} {\implies}\\\;\\\implies \overset{\frown}{AC} = \overset{\frown}{BD}\implies AC = BD\\\;\\
\left.
\begin{array}{ll}
m(\measuredangle ACD) = m(\measuredangle ABD) \\
m(\measuredangle APC) = m(\measuredangle BPD) = 90^\circ\\
AC = BD
\end{array}
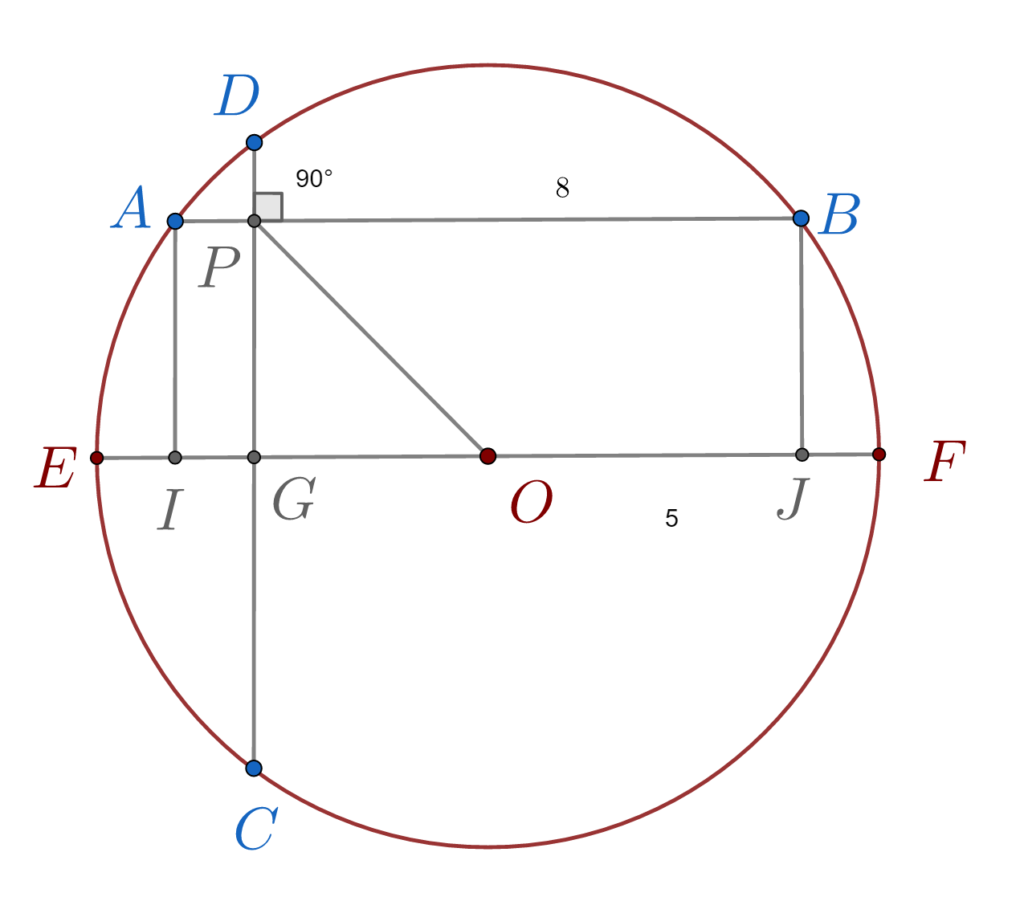
\right \} \overset{IU}{\implies}\\\;\\\overset{IU}{\implies} △ APC \equiv△ DPB \implies \\\;\\ \implies AP = DPPentru a găsi lungimea segmentului OP vom construi întâi diametrul paralel cu AB. Acesta va intersecta cercul în punctele E și F și coarda DC în G. Vom duce de asemenea și perpendicularele pe diametrul EF din punctele A și B. Ele vor intersecta EF în I, respectiv J. Folosind proprietățile arcelor și coardelor cercului arătăm că PD = 1, deci și AP =1.
\left.
\begin{array}{ll}
EF \parallel AB\\
AI \perp EF\\
BJ \perp EF
\end{array}
\right \}
\implies\\\;\\\implies\;ABJI\; dreptunghi\implies \\\;\\
\implies\left\{
\begin{array}{ll}
AI=BJ \\
AB = IJ\\
\end{array}
\right .\\\;\\AB = 8\implies IJ = 8\\\;\\
\left.
\begin{array}{ll}
EF = 2 \cdot OF\\
OF = 5
\end{array}
\right \} \implies EF = 10Știm că arcele cuprinse între două coarde paralele sunt congruente și de asemenea că la arce congruente corespund coarde congruente și demonstrăm ca EI este egal cu JF.

AB \parallel EF \implies
\overset{\frown}{AE} = \overset{\frown}{BF} \implies \\\;\\
\left.
\begin{array}{ll}
\implies AE=BF\\
\;\;\;\;\;\;\;\;\;AI=BJ\\
\;\;\;\;\;\;\;\;\;m(\measuredangle AIE) = m(\measuredangle BJF) = 90^{\circ}
\end{array}
\right \} \overset{CC}{\implies}\\\;\\
\left.
\begin{array}{ll}
\overset{CC}{\implies}EI = JF\\
\;\;\;\;\;\;\;\;EI +IJ+JF = EF\\
\;\;\;\;\;\;\;\;EF = 10\\
\;\;\;\;\;\;\;\;IJ = 8
\end{array}
\right \}{\implies}\\\;\\
\implies 10 = 2\ \cdot EI+8{\implies}\\\;\\
\implies 2\ \cdot EI= 2 {\implies}\\\;\\
\left.
\begin{array}{ll}
\implies EI =1 \\\;\;\;\;\;\;\;\;\;EO = 5\\\;\;\;\;\;\;\;\;\;EO = EI +IO\end{array}
\right \}\implies \\\;\\ \implies IO = 4
Știm de asemenea că raza AO are dimensiunea 5, am arătat ca IO este 4. Vom calcula AI aplicând teorema lui Pitagora în triunghiul AIO
AI \perp EF \implies \\ \;\\
\left.
\begin{array}{ll}
\implies △ AIO \;△ dreptunghic\\
\;\;\;\;\;\;\;\;AO =5 \;(rază)\\
\;\;\;\;\;\;\;\;IO=4\\
\end{array}
\right \}\overset{th. Pitagora}{\implies}\\\;\\\overset{th. Pitagora}{\implies}AO^2=AI^2+IO^2\implies \\\;\\\implies AI^2= 25-16\implies \\\;\\\implies AI^2 = 9\implies AI = 3
AIGP este dreptunghi deci AI este egal cu PG iar diametrul perpendicular pe coarda injumatateste coarda deci DG este 4 de unde găsim că DP = 1.
\left.
\begin{array}{ll}
PG \perp EF\\
AI \parallel DC\\
AB \parallel EF
\end{array}
\right \}\implies AIGP\; dreptunghi \implies \\ \;\\
\left.
\begin{array}{ll}
\implies AI = PG \\
\;\;\;\;\;\;\;\;\;AI = 3
\end{array}
\right \}\implies PG =3
\\\;\\
\left.
\begin{array}{ll}
EF \;diametru \\
EF \perp CD\\
CD coardă
\end{array}
\right \}\implies
\\\;\\
\left.
\begin{array}{ll}
\implies DG = \frac{CD}{2} \\\;\\
\;\;\;\;\;\;\;\;\;CD = 8
\end{array}
\right \}\implies
\\\;\\
\left.
\begin{array}{ll}\implies DG = 4\\
\;\;\;\;\;\;\;\;\;PG = 3\\
\;\;\;\;\;\;\;\;\;DG = DP+PG
\end{array}
\right \}\implies\\\;\\\implies PD =DG -PG \implies\\\;\\
\left.
\begin{array}{ll}
\implies PD=1\\
\;\;\;\;\;\;\;\;\;PD =AP
\end{array}
\right \}\implies\\\;\\\implies AP =1
AIGP\; dreptunghi \implies \\
\left.
\begin{array}{ll}
\implies AP =IG\\
\;\;\;\;\;\;\;\;\;AP = 1 \\
\end{array}
\right \}\implies\\\;\\
\left.
\begin{array}{ll}
\implies IG =1\\
\;\;\;\;\;\;\;\;\;IO =IG+GO\\
\;\;\;\;\;\;\;\;\;IO = 4\\
\end{array}
\right \}\implies\\\;\\
\implies GO = IG -IO \implies\\\;\\
\left.
\begin{array}{ll}
\implies GO =3\\
\;\;\;\;\;\;\;\;\;PG =3\\
△ PGO\; △ dreptunghic\\
\end{array}
\right \}\overset {th. Pitagora}{\implies}\\\;\\\overset {th. Pitagora}{\implies} PO^2 =PG^2+GO^2\implies\\\;\\\implies PO^2 = 3^2+3^2\implies\\\;\\\implies PO^2 = 2\cdot3^2\implies \\
\;\\PO = 3\cdot\sqrt[]{2}[the_ad_group id=”102″]