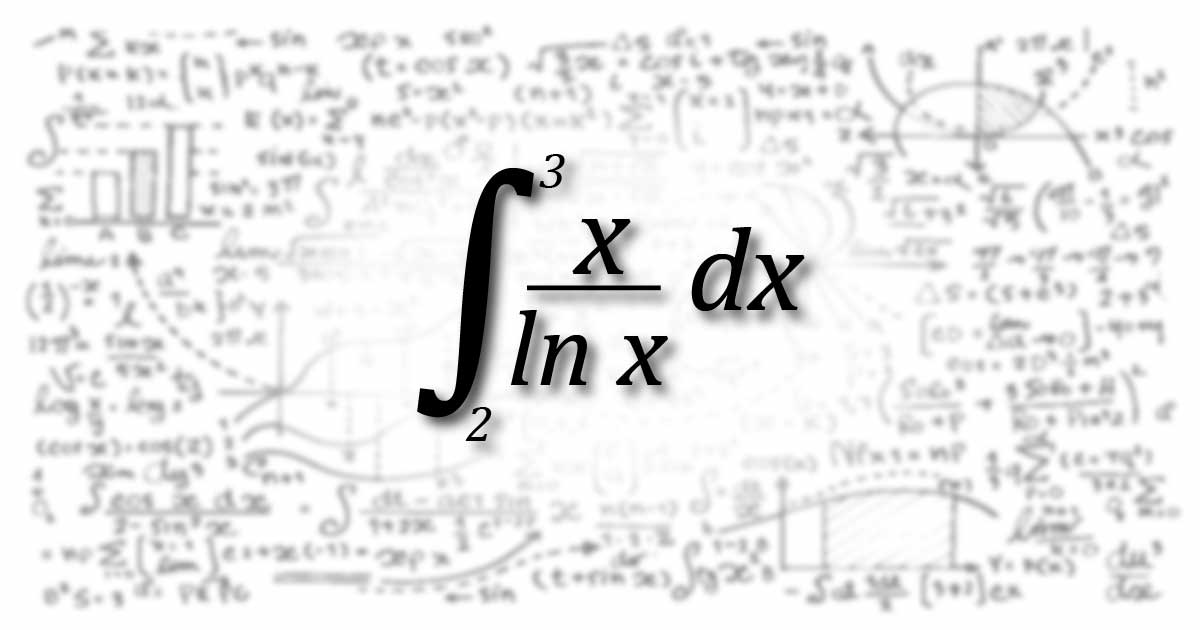Problemă rezolvată dintre subiectele date la clasa a XII-a la ONGM 2020-2021, București.
Enunț
Dacă a este partea întreagă a numărului b = \displaystyle {\int _2^{3}\dfrac{x}{lnx} dx } \ atunci:\\[1em] A. \ a = 0 \quad B. \ a = 1 \\ C.\ a = 2 \quad D.\ a = 3 \\E. \ a = 4
Rezolvare
Pentru a rezolva aceasta problemă vom aplica teorema de medie
f : [m, n] \to \mathbf R, \textbf{ funcție continuă }\implies \\ \\[1em] \implies
(\exists)\ q \in [m, n], \text{a. î} \\[1em] \ \int _m^{n} f(x) dx = (n-m)\cdot f(q)\dfrac{x}{lnx} \text{ este continuă pe intervalul [2, 3]} \implies \\ (\exists)\ c \in [2, 3], \text{a. î} \\[1em] \int _2^{3} f(x) dx = (3-2)\cdot f(c) \implies \\[1em] \implies b = \dfrac{c}{lnc}În continuare vom vom studia monotonia funcției f.
f(x) = \dfrac{x}{lnx}, f: [2, 3] \to \mathbf R f este derivabilă deoarece x și ln x sunt derivabile pe [2,3].
f'(x) = \bigg(\dfrac{x}{lnx}\bigg)' = \\[1em] =\dfrac{x' \cdot lnx - x \cdot (lnx)'}{ln^2x} = \\ \; \\=\dfrac{1 \cdot lnx - \cancel x \cdot \dfrac{1}{\cancel x}}{ln^2x} = \dfrac{lnx - 1}{ln^2x}Semnul lui f'(x) va fi dat de valorea lui lnx -1 (ln2x este mereu pozitiv). Funcția ln x- 1 este crescătoare și este 0 când x este e. e aparține intervalului [2, 3]. Vom analiza monotonia în tabelul de mai jos:
\begin{array}{|r|c|c|c|l|l|l|l| } \hline
x &2\ \ \ \ \ &e &\ \ \ \ \ 3 \\ \hline
f(x) &\frac{2}{ln2}\searrow &e& \nearrow \frac{3}{ln3}\\\hline
f'(x) &---- &0 &++++\\
\hline
\end{array}Studiind monotonia funcției observăm că f are un punct de minim în e, iar valorile funcției vor fi mai mari decât f(e) care este e și sunt mai mici decât valoarea maxima dintre f(2) și f(3). Presupunem f(2) < f(3).
\dfrac{2}{ln2} < \dfrac{3}{ln3} \iff 2\cdot ln3 < 3 \cdot ln2\iff \\[1em] \iff ln 3^2 < ln 2^3 \cdot 9 < 8\ (fals) \implies \\[1em] \implies\dfrac{2}{ln2} > \dfrac{3}{ln3} \implies \\[1em] \implies (\forall) x \in [2, 3],\ \ \ e \leq f(x) \leq \dfrac{2}{ln2}În continuare vom demonstra că f(2) < 3:
\dfrac{2}{ln2} < 3 \iff 2 < 3 \cdot ln 2\iff \\[1em] \iff 2 < ln 2^3 \iff ln e^2 < ln 2^3 \iff \\[1em] \iff e^2 < 2^3 \\[1em]
e \approx 2.71, \implies e^2 \approx 7.389 Am demonstrat ca e ≤ f(x) < 3 pentru oricare x ∈ [2,3]
\left .
\begin{array}{ll}
e \leq f(x) <3, (\forall) x \in [2,3] \\[1em]
b = f(c), \ c \in [2,3]
\end{array}
\right \} \implies \\[1em] \implies 2\leq b < 3
\implies \\[1em] \implies
[b] = 2Răspunsul corect este C, 2.