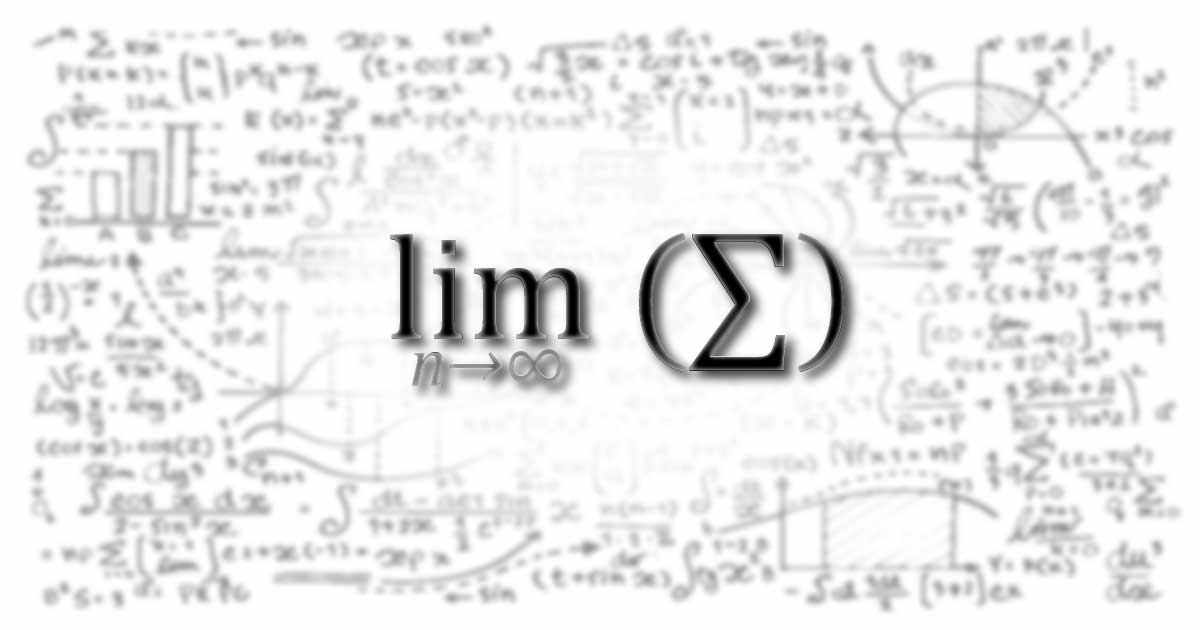Problema rezolvată #32 – ONGM 2020-2021

 \displaystyle{\lim_{n\to\infty} } \bigg(\dfrac{1^2\cdot 2}{n^4 +n} + \dfrac{2^2\cdot3}{n^4 +2\cdot n}+ ... +\dfrac{n^2\cdot(n+1)}{n^4 + n^2} \bigg)

 \text{A. }\dfrac{1}{4}    \qquad \text{B. } \dfrac{1}{3} \qquad  \text{C. }  \infty  \qquad  \text{D.   } 0 \qquad

\dfrac{1^2\cdot 2}{n^4 +n} + \dfrac{2^2\cdot3}{n^4 +2\cdot n}+ ... +\dfrac{n^2\cdot(n+1)}{n^4 + n^2} = \\ \; \\= \displaystyle {\sum_{k=1}^n}\dfrac{ k^2\cdot(k+1)}{n^4 + n\cdot k}\\ \; \\ \\ \; \\
\dfrac{ k^2\cdot(k+1)}{n^4 + n^2} \leq  \\  \; \\ \leq\dfrac{ k^2\cdot(k+1)}{n^4 + n\cdot k} \leq  \\  \; \\ \leq\dfrac{ k^2\cdot(k+1)}{n^4 + n } \implies  \\ \; \\  \; \\ \implies  \displaystyle {\sum_{k=1}^n}\dfrac{ k^2\cdot(k+1)}{n^4 + n^2} \leq  \\  \; \\ \leq\displaystyle {\sum_{k=1}^n}\dfrac{ k^2\cdot(k+1)}{n^4 + n\cdot k} \leq \\  \; \\ \leq \displaystyle {\sum_{k=1}^n}\dfrac{ k^2\cdot(k+1)}{n^4 + n } \implies \newline \ \newline \ \newline\  \implies  \displaystyle \dfrac{1}{{n^4 + n^2}}{\sum_{k=1}^n} { k^2\cdot(k+1)} \leq \\  \; \\ \leq   \displaystyle {\sum_{k=1}^n}\dfrac{ k^2\cdot(k+1)}{n^4 + n\cdot k} \leq \\  \; \\ \leq   \displaystyle \dfrac{1}{{n^4 + n}}{\sum_{k=1}^n} { k^2\cdot(k+1)} \implies \newline \; \newline \;  \implies  \displaystyle \dfrac{1}{{n^4 + n^2}}{\sum_{k=1}^n} { (k^3 +k^2)} \leq  \\  \; \\ \leq \displaystyle {\sum_{k=1}^n}\dfrac{ k^2\cdot(k+1)}{n^4 + n\cdot k} \leq  \\  \; \\ \leq \displaystyle \dfrac{1}{{n^4 + n}}{\sum_{k=1}^n} {(k^3 +k^2)} \implies  \\ \; \\  \; \\\implies  \displaystyle \dfrac{1}{{n^4 + n^2}}\bigg( {\sum_{k=1}^n} k^3 +\sum_{k=1}^n k^2 \bigg) \leq \\  \; \\  \leq \displaystyle {\sum_{k=1}^n}\dfrac{ k^2\cdot(k+1)}{n^4 + n\cdot k} \leq  \\ \; \\ \leq \displaystyle \dfrac{1}{{n^4 + n}}\bigg( {\sum_{k=1}^n} k^3 +\sum_{k=1}^n k^2 \bigg)  \newline \newline \newline

 {\sum_{k=1}^n} k^3  =  \bigg( \dfrac{n \cdot (n+1) }{2} \bigg)  ^2   \; \\[2em]
 {\sum_{k=1}^n} k^2  =  \dfrac{n \cdot (n+1) \cdot(2n+1)}{6}  \newline \;\newline \newline
 \implies \sum_{k=1}^n k^3  +  \sum_{k=1}^n k^2 = \\ \; \\ = \dfrac{n^2 \cdot (n+1)^2 }{4} +  \dfrac{n \cdot (n+1) \cdot(2n+1)}{6}  =  \\ \; \\ =\dfrac{3 \cdot n^2 \cdot (n+1)^2  + 2 \cdot n \cdot (n+1) \cdot(2n+1)}{12} =    \\ \; \\ =\dfrac{3 \cdot n^2 \cdot (n+1)^2  + 2 \cdot n \cdot (n+1) \cdot(2n+1)}{12} = \\ \; \\ = \dfrac{ n \cdot (n+1) \cdot (3 \cdot n \cdot (n+1)   + 2 \cdot(2n+1))}{12} =   \\ \; \\  = \dfrac{ n \cdot (n+1) \cdot (3 n ^2 +3n + 4n+2)}{12} = \\ \; \\ = \dfrac{ (n^2 + n) \cdot (3 n ^2 +7n+2)}{12} = \\ \; \\ = \dfrac{ 3n ^4 +7n^3+2n^2 + 3 n ^3 +7n^2+2n}{12} =   \\ \; \\ =\dfrac{ 3n ^4 +10n^3+9n^2 +2n}{12} 

 \dfrac{1}{{n^4 + n^2}} \cdot \dfrac{ 3n ^4 +10n^3+9n^2 +2n}{12}  \leq  \\ \; \\  \leq  \displaystyle {\sum_{k=1}^n}\dfrac{ k^2\cdot(k+1)}{n^4 + n\cdot k} \leq  \\ \; \\  \leq \displaystyle \dfrac{1}{{n^4 + n}} \cdot \dfrac{ 3n ^4 +10n^3+9n^2 +2n}{12}   \implies \\ \; \\ \implies 
 \displaystyle{\lim_{n\to\infty} \dfrac{ 3n ^4 +10n^3+9n^2 +2n}{12 \cdot(n^4 + n^2)} } \leq  \\ \; \\  \leq \displaystyle{\lim_{n\to\infty} \displaystyle {\sum_{k=1}^n}\dfrac{ k^2\cdot(k+1)}{n^4 + n\cdot k} }\leq  \\ \; \\  \leq \displaystyle{\lim_{n\to\infty} \dfrac{ 3n ^4 +10n^3+9n^2 +2n}{12 \cdot(n^4 + n)} } \implies\\ \; \\   \implies \dfrac{3}{12}  \leq \displaystyle{\lim_{n\to\infty} \displaystyle {\sum_{k=1}^n}\dfrac{ k^2\cdot(k+1)}{n^4 + n\cdot k} }\leq  \dfrac{3}{12}  \implies  \\ \; \\   \implies  \displaystyle{\lim_{n\to\infty} \displaystyle {\sum_{k=1}^n}\dfrac{ k^2\cdot(k+1)}{n^4 + n\cdot k} } =  \dfrac{1}{4}

 \text{Răspunsul este } \textbf{A},  \dfrac{1}{4}. \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad